基于模型的增强学习:框架
如何学习系统转移概率$f(\mathbf{s},\mathbf{a})$。
v0.5
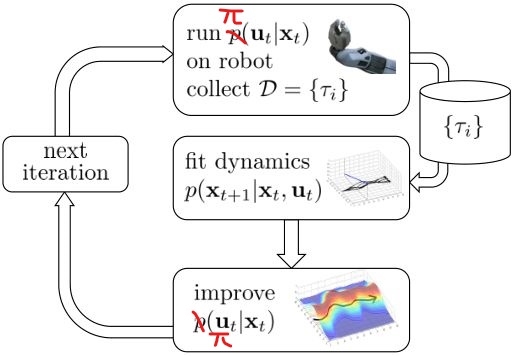
如果我们知道模型动态$f(\mathbf{s}_ t,\mathbf{a}_ t)=\mathbf{s}_ {t+1}$,或者随机的分布$p(\mathbf{s}_{t+1}\vert \mathbf{s}_t,\mathbf{a}_t)$,那么我们就可以使用上一篇的方法。因此我们考虑去从数据中学习$f(\mathbf{s}_t,\mathbf{a}_t)$,这样的方法被统称为基于模型的增强学习(model-based reinforcement learning),其基本步骤为(v0.5):
- 运行某种基本策略$\pi_0(\mathbf{a}_t\vert \mathbf{s}_t)$(如随机策略)来收集样本数据$\mathcal{D}=\lbrace(\mathbf{s},\mathbf{a},\mathbf{s}’)_i\rbrace$。
- 通过最小化$\sum_i\Vert f(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{s}_i’\Vert^2$的方法来学习模型动态$f(\mathbf{s},\mathbf{a})$。
- 根据$f(\mathbf{s},\mathbf{a})$来计划未来行动。
这是经典机器人学系统识别(system identification)中使用的方法,即已经有了参数式的机器人的运动方程,需要收集数据来估计参数,收集数据的基本策略可以是随机的。 这个方法在我们已知准确的模型系统动态方程,且只有个别(如10-30个)参数不知道的情况下还是很好用的。 v0.5版本有个严重的问题:分布不匹配(类似模仿学习)。我们通过分布$p_{\pi_0}(\mathbf{x}_ t)$来收集数据,但是实际用于规划行动时,我们遇到的是$p_{\pi_f}(\mathbf{x}_ t)$。即便我们训练了一个在分布$p_{\pi_0}(\mathbf{x}_ t)$下很好的模型,但这个模型在$p_{\pi_f}(\mathbf{x}_t)$所遇到的状态下可以很差。并且,这样的分布不匹配问题在使用越具表达力的模型簇时越严重。如果像我们跟前面所说的一样只缺少几个待定参数,那么其实对数据要求还是不高的;而使用如深度神经网络这样具有高表达力的模型,则会把红色部分的数据拟合得相当好(过拟合),然后产生更大的问题。
v1.0
收集更多“实际分布”下的数据,改进的(v1.0)版本如下:
- 运行某种基本策略$\pi_0(\mathbf{a}_t\vert \mathbf{s}_t)$(如随机策略)来收集样本数据$\mathcal{D}=\lbrace(\mathbf{s},\mathbf{a},\mathbf{s}’)_i\rbrace$。
- 通过最小化$\sum_i\Vert f(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{s}_i’\Vert^2$的方法来学习模型动态$f(\mathbf{s},\mathbf{a})$。
- 根据$f(\mathbf{s},\mathbf{a})$来计划未来行动。
- 执行这些行动,并得到一系列结果数据$\lbrace(\mathbf{s},\mathbf{a},\mathbf{s}’)_j\rbrace$加入到$\mathcal{D}$中。反复执行2-4步。
与DAgger不同,DAgger收集到新数据需要重新标注,希望新数据的轨迹和以前的一致,避免偏差。
v1.5
考虑进一步的改进。错误并不只是致命错误,对于小错误,我们希望当小错误累积到一定程度时,重新规划方法。v1.5版本如下:
- 运行某种基本策略$\pi_0(\mathbf{a}_t\vert \mathbf{s}_t)$(如随机策略)来收集样本数据$\mathcal{D}=\lbrace(\mathbf{s},\mathbf{a},\mathbf{s}’)_i\rbrace$。
- 通过最小化$\sum_i\Vert f(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{s}_i’\Vert^2$的方法来学习模型动态$f(\mathbf{s},\mathbf{a})$。
- 根据$f(\mathbf{s},\mathbf{a})$来计划未来行动。(如使用iLQR)
- 基于MPC的思想??????,仅执行计划中的第一步行动,观察到新的状态$\mathbf{s}’$。
- 将这一组新的$(\mathbf{s},\mathbf{a},\mathbf{s}’)$加入到$\mathcal{D}$中。反复执行若干次3-5步之后,回到第2步重新学习模型。
第3步规划得越频繁,就越可以容忍更差的模型和更糟糕的规划方法。这种方法优点在于对小的模型误差鲁棒性较好,在模型不准确的时候也可以得到很好的控制;缺点在于它的计算代价比较大,需要一边在线运行规划算法,一边收集数据。
v2.0
在这个v1.5版本中,最难的一点是做规划。越精密的模型和方法,计划未来行动的代价越大。MPC方法可能很好,但是计算代价有可能会很大,因此采用构造一个策略函数$\pi_\theta(\mathbf{s}_t)$的方法来得到具体的行动,即v2.0版本:
- 运行某种基本策略$\pi_0(\mathbf{a}_t\vert \mathbf{s}_t)$(如随机策略)来收集样本数据$\mathcal{D}=\lbrace(\mathbf{s},\mathbf{a},\mathbf{s}’)_i\rbrace$。
- 通过最小化$\sum_i\Vert f(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{s}_i’\Vert^2$的方法来学习模型动态$f(\mathbf{s},\mathbf{a})$。
- 通过$f(\mathbf{s},\mathbf{a})$,使用反向传播的方法来优化策略函数$\pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)$。
- 执行$\pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)$,将新的$(\mathbf{s},\mathbf{a},\mathbf{s}’)$加入到$\mathcal{D}$中。反复执行2-4步。

在第3步,我们不再是用某种方法来规划未来路径,而是使用收益的梯度通过反向传播的方法来优化策略函数。这种方法优点在于它在运行时计算代价较小,只需要根据策略函数执行行动,比规划算法容易很多;缺点在于它可能在数值上非常不稳定,尤其是在一些随机域之中。
模型簇的选择
- 高斯过程
- 优点:强化学习前期经常因为缺少数据而过拟合,高斯过程的数据利用率很高
- 缺点:不适合非光滑系统,大数据情况下计算慢
- 神经网络
- 优点:模型表现力强,适合高维数据
- 缺点:早期训练时数据量小导致过拟合
- 高斯混合模型
- 优点:适合线性模型
Nagabandi et al. (2017)使用神经网络进行模拟机器人控制。基于模型的方法使用12k个样本点达到收益函数900,而无模型的方法通过4m-12m个样本点达到收益函数4800;这个例子清晰地告诉我们两者区别原因在于基于模型的方法尝试的是提高模型拟合程度(需要的样本数可能只是无模型的百分之一、千分之一),而无模型的方法则是去提高收益函数。
从全局模型到局部模型
之前讨论的模型是全局模型,即学习的$f(\mathbf{s}_t,\mathbf{a}_t)$对整个系统都起作用。出于这个目的,我们使用神经网络去拟合。它的问题在于:如果一开始估计错误,它会去探索因模型错误而被乐观估计的区域,这是因为大多数状态模型能很好地估计,总有一些状态模型会出错误。某些情况下,模型比行动策略要复杂,比如拿杯子,策略很简单,模型却要考虑各种物理关系等等。因此,有时我们想训练一个局部模型,得到梯度$\frac{\mathrm{d}f}{\mathrm{d}\mathbf{x}_t}, \frac{\mathrm{d}f}{\mathrm{d}\mathbf{u}_t}$等局部信息,方便用iLQR做轨迹优化。
我们需要梯度信息$\frac{\mathrm{d}f}{\mathrm{d}\mathbf{x}_ t},\frac{\mathrm{d}f}{\mathrm{d}\mathbf{u}_ t}$。假设模型动态是一个高斯分布$p(\mathbf{x}_{t+1}\vert \mathbf{x}_t,\mathbf{u}_t)=\mathcal{N}(f(\mathbf{x}_t,\mathbf{u}_t),\Sigma)$,其中$f(\mathbf{x}_t,\mathbf{u}_t)\approx \mathbf{A}_t\mathbf{x}_t+\mathbf{B}_t\mathbf{u}_t$。这样的假设保证给定时间内均值是线性的,并且只需拟合$(\mathbf{A}_t,\mathbf{B}_t)$,就能得到微分信息,并使用iLQR方法改进策略函数$\pi(\mathbf{u}_t\vert \mathbf{x}_t)$。
使用怎样的策略收集数据?
由于目前使用局部模型,因此随机选择策略很难拟合当前策略的局部信息。对于ILQR,最优控制策略是$\mathbf{u}_ t=\mathbf{K}_ t(\mathbf{x}_ t-\hat{\mathbf{x}}_ t)+\mathbf{k}_ t+\hat{\mathbf{u}}_ t$,我们选择高斯分布策略$\pi(\mathbf{u}_ t|\mathbf{x}_ t)=\mathcal{N}(\mathbf{K}_ t(\mathbf{x}_ t-\hat{\mathbf{x}}_ t)+\mathbf{k}_ t+\hat{\mathbf{u}}_ t,\Sigma_t)$,对最优策略加入了些噪音,数据多样性得到增强。对于方差,我们想得到不同的轨迹,但也不要完全不同,一个建议是$\Sigma_ t=\mathbf{Q}_ {\mathbf{u}_ t,\mathbf{u}_ t}^{-1}$。这样,我们的目标就是找到噪音最大但代价最小的策略(双目标规划),即策略尽可能随机,但同时保持高收益。目标函数$\min\sum_{t=1}^Tc(\mathbf{x}_ t,\mathbf{u}_ t)$等价于$\min\sum_{t=1}^T\mathbf{E}_{(\mathbf{x}_t,\mathbf{u}_t)\sim \pi(\mathbf{x}_t,\mathbf{u}_t)}[c(\mathbf{x}_t,\mathbf{u}_t)-\mathcal{H}(\pi(\mathbf{u}_t|\mathbf{x}_t))]$ (解释看不懂,见PPT???)
如何拟合局部模型
我们使用高斯分布形式的模型动态,最简单的方法是直接使用线性回归$p(\mathbf{x}_{t+1}|\mathbf{x}_t,\mathbf{u}_t)=\mathcal{N}(\mathbf{A}_t\mathbf{x}_t+\mathbf{B}_t\mathbf{u}_t+\mathbf{c},\mathbf{N}_t)$。考虑到相近时间内动态模型是接近的,贝叶斯线性回归是更好的选择。利用所有数据拟合全局模型(GP,neural network,GMM),然后把它作为先验,以提高数据使用率。
全局模型需要更多的数据,而局部模型在每次策略更新后都需要推倒重来,因此这里面存在一个权衡。
策略变化太大怎么办?
对于局部模型,它只关注局部信息,如果策略变化过大,可能会完全偏离目标。因此我们需要使新的策略与原策略接近。如果两个轨迹相近,那么动态模型也会比较接近,因此可以加上两个轨迹KL散度的限制(无模型增强学习中也很常见,如TRPO)。
推导得到$D_{\mathrm{KL}}(p(\tau)\Vert\bar{p}(\tau))=\sum_{t=1}^T\mathbf{E}_{p(\mathbf{x}_t,\mathbf{u}_t)}[-\log\bar{\pi}(\mathbf{u}_t\vert\mathbf{x}_t)-\mathcal{H}(\pi(\mathbf{u}_t\vert\mathbf{x}_t))]$。KL散度表达式和之前的目标函数很类似,可以用拉格朗日乘子法解决。略。