- 基于模型的方法
- 随机优化(stochastic optimization)
- 蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)
- 轨迹优化(Trajectory Optimization)
- 总结
基于模型的方法
知道系统转移概率的情况下,如何进行行动决策
在之前的增强学习算法中,我们都假设初始状态、转移概率未知,因为它很难知道。但在某些情况下,系统转移概率(dynamics)是相对容易得到的,比如游戏中状态会根据具体的规则而改变,如果我们能知道这些系统转移概率,通常问题就会变得简单很多。基于模型的(model-based)增强学习方法通过学习系统转移概率来决定如何选择行动。在这一篇中,我们将先介绍知道系统转移概率的情况下,如何进行行动决策(最优控制、轨迹优化);之后,我们再去关注如何去学习未知的转移概率,以及如何通过诸如模仿最优控制的方法学习策略。
假设环境是确定性的,我们做的是最优控制,一系列行为决策可以表示为:
如果环境是随机的,轨迹条件概率为$p_\theta(\mathbf{s}_ 1,\ldots,\mathbf{s}_ T\vert \mathbf{a}_ 1,\ldots,\mathbf{a}_ T)=p(\mathbf{s}_ 1)\prod_{t=1}^Tp(\mathbf{s}_ {t+1}\vert \mathbf{s}_ t,\mathbf{a}_ t)$,则之前的期望收益最大的开环(open-loop)控制系统$\mathbf{a}_ 1,\ldots,\mathbf{a}_ T=\arg\max_{\mathbf{a}_ 1,\ldots,\mathbf{a}_ T}\mathbf{E}\left[\sum_{t=1}^Tr(\mathbf{s}_t,\mathbf{a}_t) \vert \mathbf{a}_1,\ldots,\mathbf{a}_T\right]$就不见得是最优的了:因为没必要一下做所有决策,可以做一步决策,并根据环境反馈进行修正,这称为闭环。开环系统在一开始就把所有决策单向传递给环境,不接受反馈;闭环系统则每次只传递单次行动,并接受下一个状态作为反馈。
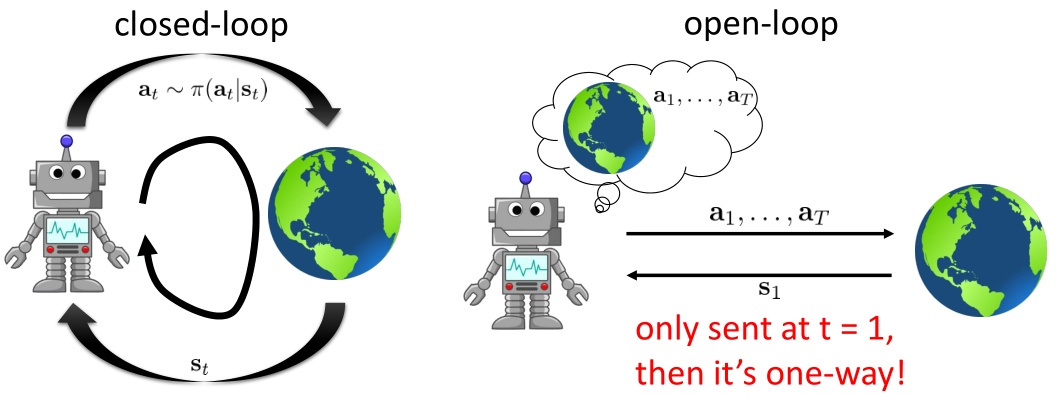
在闭环系统中,轨迹概率为$p(\mathbf{s}_ 1,\mathbf{a}_ 1,\ldots,\mathbf{s}_ T,\mathbf{a}_ T)=p(\mathbf{s}_ 1)\prod_{t=1}^T\pi(\mathbf{a}_ t\vert\mathbf{s}_ t)p(\mathbf{s}_ {t+1}\vert \mathbf{s}_ t,\mathbf{a}_ t)$,目标为找到最优策略$\pi=\arg\max_\pi\mathbf{E}_ {\tau\sim p(\tau)}\left[\sum_{t=1}^Tr(\mathbf{s}_t,\mathbf{a}_t)\right]$。之前的算法用神经网络表示策略(全局),这一篇中我们将使用经典的轨迹优化(trajectory optimization)方法来训练一个线性策略簇$\mathbf{K}_t\mathbf{s}_t+\mathbf{k}_t$(局部),基本上就是主要执行$\mathbf{k}_t$,并使用当前给定状态做出一些线性修正。根据限定的策略簇不同,策略的学习可以从非常简单到非常复杂。
随机优化(stochastic optimization)
第一类规划算法是随机优化,通常用于时长比较短的问题。定义决策序列为$\mathbf{A}$,优化目标是$\mathbf{A}=\arg\max_\mathbf{A}J(\mathbf{A})$(开环)。第一种方法是从某种分布(如均匀分布)中挑选若干个决策序列$\mathbf{A}_1,\ldots,\mathbf{A}_N$,然后优化,这又称为随机打靶法(random shooting method),在低维问题中效果还不错。
第二种方法称为交叉熵方法(Cross-entropy Method, CEM),对30到50维这样的问题效果不错。具体算法如下:
- 从先验分布$p(\mathbf{A})$中抽样:$\mathbf{A}_1,\ldots,\mathbf{A}_N$。
- 计算$J(\mathbf{A}_1),\ldots,J(\mathbf{A}_N)$。
- 选取一个M<N(也可以选一个比例),挑选出J值最大的子集$\mathbf{A}_ {i_1},\ldots,\mathbf{A}_ {i_M}$。
- 用$\mathbf{A}_ {i_1},\ldots,\mathbf{A}_ {i_M}$重新拟合先验分布$p(\mathbf{A})$。循环1。
我们拟合的分布通常为多元高斯分布。优点是简单易并行,缺点是维度一大会很容易错过表现好的抽样区域,且只能处理开环规划的问题。
蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)
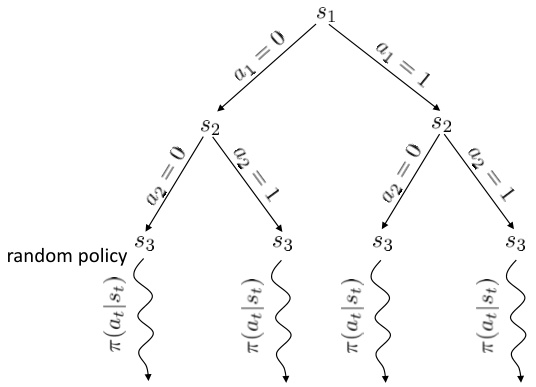
蒙特卡洛树搜索适合求解闭环控制的离散决策问题。根据每次的状态和操作,会形成一颗巨大的树。对这棵树不能暴力搜索,而是在到一定阶段后,使用一些随机策略来评估这些叶子节点的好坏。从每个叶子节点出发继续执行这个策略若干步来看最后结果怎样,来大概给这个叶子节点的效果打个分。注意,此时复杂度不再是指数级别的,而是叶子的个数乘上启发式策略运行长度。这个方法的基本思想是,如果当前已经进入了一个优势很大的局面,那么一些比较菜的策略也应该能把优势保持到最后;反之亦然。因此,实际中做MCTS的时候通常选择的就是随机策略,选一个很好的策略通常是次要的。MCTS的一般结构为:
- 假设当前决策的根节点为$s_1$,使用某种TreePolicy($s_1$)得到一个叶子节点$s_l$。
- 使用某种随机策略(或其他)DefaultPolicy($s_l$)评估该叶子节点。
- 更新在$s_1$到$s_l$路径上的所有值,并返回第一步重新循环若干次。
- 循环1-3若干次后,从根节点$s_1$的所有决策中找一个评分最高的。
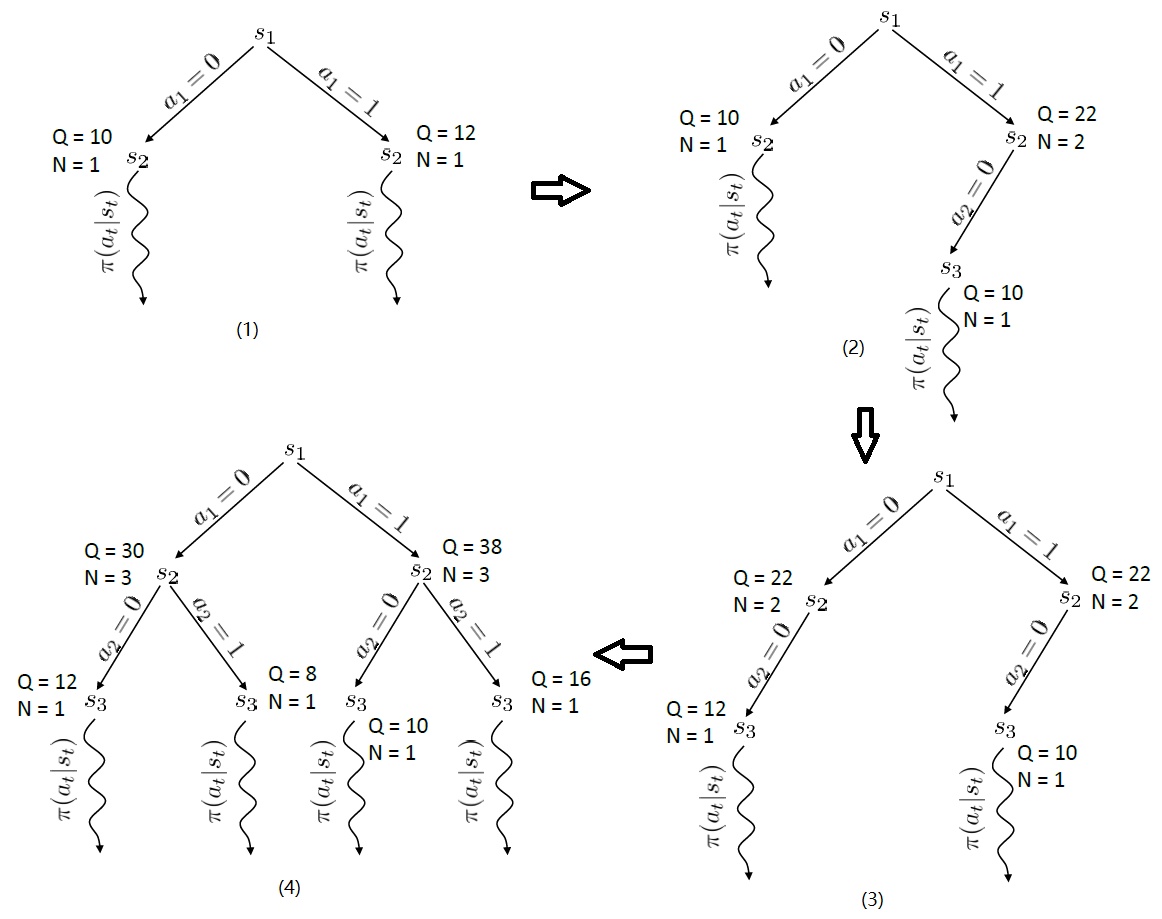
TreePolicy有很多,其中一个很流行的UCT(Upper Confidence Bounds for Trees):如果$s_t$没有完全被展开,那么选择一个没有评估过的新行动$a_t$;否则就选取一个得分最大的儿子$s_{t+1}$,其中得分公式为$\text{Score}(s_{t+1})=\frac{Q(s_{t+1})}{N(s_{t+1})}+2C\sqrt{\frac{2\ln N(s_t)}{N(s_{t+1})}}$,越大越好,$Q(s_t)$为该节点为跟的子树的所有已经被展开过的节点的评分之和,$N(s_t)$为该节点为根的子树中已经被展开过的节点个数,因此$\frac{Q(s_t)}{N(s_t)}$就是$s_t$的平均评分了;后者则是用来评估稀有性。
轨迹优化(Trajectory Optimization)
轨迹优化是连续控制中的重要问题。使用控制的记号,记问题为:
对于约束问题,可以展开为复杂的非约束表达式:
方便基于梯度的优化算法。因此只需要以下几个梯度:$\frac{\mathrm{d}f}{\mathrm{d}\mathbf{x}_t},\frac{\mathrm{d}f}{\mathrm{d}\mathbf{u}_t},\frac{\mathrm{d}c}{\mathrm{d}\mathbf{x}_t},\frac{\mathrm{d}c}{\mathrm{d}\mathbf{u}_t}$。
实际中使用一阶方法不是很好,原因在于:第一次行动$\mathbf{u}_1$在表达式出现很多次,因此$\mathbf{u}_1$相对重要,而最后一次行动影响变小,产生病态的梯度信息。好消息是有一些非常有效的二阶算法。
关于轨迹优化有两类方法,一类是shooting method,它只优化每一时刻的行动$\mathbf{u}_ t$,而把状态$\mathbf{x}_ t$看作是行动产生的结果,本质上就是$\min_{\mathbf{u}_1,\ldots,\mathbf{u}_T}c(\mathbf{x}_1,\mathbf{u}_1)+c(f(\mathbf{x}_1,\mathbf{u}_1),\mathbf{u}_2)+\ldots+c(f(\ldots),\mathbf{u}_T)$。它不稳定,行动的稍微变化就会使轨迹发生大的变化。
另一种是collocation method,同时优化每个时刻的状态和行动,并使用约束来将状态和行动维系起来(甚至有时候只优化状态,而把行动看成状态转移的手段),本质上就是$\min_{\mathbf{u}_ 1,\ldots,\mathbf{u}_ T,\mathbf{x}_ 1,\ldots,\mathbf{x}_ T}\sum_{t=1}^Tc(\mathbf{x}_ t,\mathbf{u}_ t)~\text{s.t.}~\mathbf{x}_ t=f(\mathbf{x}_ {t-1},\mathbf{u}_{t-1})$。它更加稳定,但约束条件使得难以求解。
对于线性动态系统可以使用LQR(Linear Quadratic Regulator)。
从T时刻向前依次计算参数,由$\nabla_{\mathbf{u}_T}Q(\mathbf{x}_T,\mathbf{u}_T)=0$可以把最优决策$\mathbf{u}_T$写成$\mathbf{x}_T$的函数:$\mathbf{u}_T=\mathbf{K}_T\mathbf{x}_T+\mathbf{k}_T$,然后带入消元得到最优$V(\mathbf{x}_T)$。依次向前计算每一时刻。具体算法为:
- $\mathbf{Q}_ t=\mathbf{C}_ t+\mathbf{F}_ t^\top\mathbf{V}_ {t+1}\mathbf{F}_ t$,$\mathbf{q}_ t=\mathbf{c}_ t+\mathbf{F}_ t^\top\mathbf{V}_ {t+1}\mathbf{f}_ t+\mathbf{F}_ t^\top\mathbf{v}_{t+1}$
- $Q(\mathbf{x}_ t,\mathbf{u}_ t)=\text{const}+\frac{1}{2}\left[\begin{array}{l}\mathbf{x}_ t\\mathbf{u}_ t\end{array}\right]^\top\mathbf{Q}_ t\left[\begin{array}{l}\mathbf{x}_ t\\mathbf{u}_ t\end{array}\right]+\left[\begin{array}{l}\mathbf{x}_ t\\mathbf{u}_ t\end{array}\right]^\top\mathbf{q}_ t$,因此$\mathbf{u}_ t\leftarrow\arg\min_{\mathbf{u}_ t}Q(\mathbf{x}_ t,\mathbf{u}_ t)=\mathbf{K}_ t\mathbf{x}_ t+\mathbf{k}_ t$,其中$\mathbf{K}_ t=-\mathbf{Q}_ {\mathbf{u}_ t,\mathbf{u}_ t}^{-1}\mathbf{Q}_ {\mathbf{u}_ t,\mathbf{x}_ t},\mathbf{k}_ t=-\mathbf{Q}_ {\mathbf{u}_ t$,$\mathbf{u}_ t}^{-1}\mathbf{q}_{\mathbf{u}_t}$
- $\mathbf{V}_ t=\mathbf{Q}_ {\mathbf{x}_ t,\mathbf{x}_ t}+\mathbf{Q}_ {\mathbf{x}_ t,\mathbf{u}_ t}\mathbf{K}_ t+\mathbf{K}_ t^\top\mathbf{Q}_ {\mathbf{u}_ t,\mathbf{x}_ t}+\mathbf{K}_ t^\top\mathbf{Q}_ {\mathbf{u}_ t,\mathbf{u}_ t}\mathbf{K}_ t$, $\mathbf{v}_ t=\mathbf{q}_ {\mathbf{x}_ t}+\mathbf{Q}_ {\mathbf{x}_ t,\mathbf{u}_ t}\mathbf{k}_ t+\mathbf{K}_ t^\top\mathbf{q}_ {\mathbf{u}_ t}+\mathbf{K}_ t^\top\mathbf{Q}_{\mathbf{u}_t,\mathbf{u}_t}\mathbf{k}_t$, $V(\mathbf{x}_t)=\text{const}+\frac{1}{2}\mathbf{x}_t^\top\mathbf{V}_t\mathbf{x}_t+\mathbf{x}_t^\top\mathbf{v}_t$
其中,$Q(\mathbf{x}_ t,\mathbf{u}_ t)$代表了我们从状态$\mathbf{x}_ t$执行$\mathbf{u}_ t$后直到最后的最小代价,$V(\mathbf{x}_ t)=\min_{\mathbf{u}_t}Q(\mathbf{x}_t,\mathbf{u}_t)$是从状态$\mathbf{x}_t$出发直到最后的最小代价。求解完后,如果我们知道初始状态$\mathbf{x}_1$,就可以在每一步执行$\mathbf{u}_t=\mathbf{K}_t\mathbf{x}_t+\mathbf{k}_t$作为最优策略。
将LQR使用到非线性问题中,进行局部泰勒展开,将f做一阶展开$f(\mathbf{x}_ t,\mathbf{u}_ t)\approx f(\hat{\mathbf{x}}_ t,\hat{\mathbf{u}}_ t)+\nabla_{\mathbf{x}_ t,\mathbf{u}_ t} f(\hat{\mathbf{x}}_ t,\hat{\mathbf{u}}_ t) \left[\begin{array}{l}\mathbf{x}_ t-\hat{\mathbf{x}}_ t\\mathbf{u}_ t-\hat{\mathbf{u}}_ t\end{array}\right]$,将c做二阶展开$c(\mathbf{x}_ t,\mathbf{u}_ t)\approx c(\hat{\mathbf{x}}_ t,\hat{\mathbf{u}}_ t)+\nabla_{\mathbf{x}_ t,\mathbf{u}_ t}c(\hat{\mathbf{x}}_ t,\hat{\mathbf{u}}_ t)\left[\begin{array}{l}\mathbf{x}_ t-\hat{\mathbf{x}}_ t\\mathbf{u}_ t-\hat{\mathbf{u}}_ t\end{array}\right]+\frac{1}{2}\left[\begin{array}{l}\mathbf{x}_ t-\hat{\mathbf{x}}_ t\\mathbf{u}_ t-\hat{\mathbf{u}}_ t\end{array}\right]^\top\nabla^2_ {\mathbf{x}_ t,\mathbf{u}_ t}c(\hat{\mathbf{x}}_ t,\hat{\mathbf{u}}_ t)\left[\begin{array}{l}\mathbf{x}_ t-\hat{\mathbf{x}}_ t\\mathbf{u}_ t-\hat{\mathbf{u}}_ t\end{array}\right]$,结构与LRQ类似,只需做一个替换。这个方法叫做迭代LQR(iterative LQR, iLQR)。如果对f使用二阶展开,就是差分动态规划(Differential Dynamic Programming, DDP)。由于f通常是一个向量值函数,做二阶微分以后会变成一个张量,比较复杂,因此通常只做一阶展开。
在使用牛顿法来求解非常复杂的非线性函数时也有一些技巧。由于梯度和Hessian阵都是局部的,而实际函数并不是一个二次函数,因此在二阶展开式存在误差,通常会做一些line search。
Tassa et al. (2012)使用iLQR做模型预测控制(Model-Predictive Control)来控制模拟机器人。这并不是与深度增强学习紧密相关的,只是使用了iLQR方法。他们的控制架构是在每一步中,
- 观察状态$\mathbf{x}_t$;
- 使用iLQR来计划$\mathbf{u}_ t,\ldots,\mathbf{u}_ {t+T},来最小化\sum_{t’=t}^{t+T}c(\mathbf{x}_ {t’},\mathbf{u}_{t’})$;
- 执行$\mathbf{u}_ t$,抛弃$\mathbf{u}_ {t+1},\ldots,\mathbf{u}_{t+T}$。
在每一步中先使用iLQR对未来若干步进行计划,然后只采用第一步的策略,然后下一次重新进行多步规划。本质上它不是一个“学习”过程,所有执行内容都是在线计划的,因此能够非常好地抗新加入的外力干扰,稳定性非常好。
总结
- 基于模型的增强学习方法学习系统转移概率,然后进行行动决策。
- 几种方法
- 随机优化:随机打靶,交叉熵。开环,用于时长短情况
- 蒙特卡洛树搜索:闭环,离散
- 轨迹优化:连续
- shooting method:只优化每一时刻的行动$u_t$,不稳定
- collocation method:同时优化$u_t,x_t$,有约束,稳定
- LRQ:处理线性问题
- iLRQ:处理非线性问题