策略迭代法
对于优势函数$A^\pi(\mathbf{s}_ t,\mathbf{a}_ t)=Q^\pi(\mathbf{s}_ t,\mathbf{a}_ t)-V^\pi(\mathbf{s}_ t)$,如果我们在状态$\mathbf{s}_ t$下执行$\arg\max_{\mathbf{a}_t}A^\pi(\mathbf{s}_t,\mathbf{a}_t)$得到一个当前最好的决策,这个决策必然是期望最优的,并且和策略$\pi$无关。因此,我们有了新的策略改进的思路(即蓝色方框):
我们引入非常经典的策略迭代法(Policy Iteration, PI)。假设已知转移概率,它包含两个步骤:
- 策略评估(Policy Evaluation):计算所有的$A^\pi(\mathbf{s},\mathbf{a})$;
- 策略改进(Policy Improvement):令$\pi\leftarrow\pi’$,其中$\pi’(\mathbf{a}_ t\vert\mathbf{s}_ t)=I\left(\mathbf{a}_ t=\arg\max_{\mathbf{a}_t}A^\pi(\mathbf{s}_t,\mathbf{a}_t)\right)$。
这个过程的主要问题在于计算$A^\pi(\mathbf{s},\mathbf{a})$,而$A^\pi(\mathbf{s},\mathbf{a})=r(\mathbf{s},\mathbf{a})+\gamma\mathbf{E}[V^\pi(\mathbf{s}’)]-V^\pi(\mathbf{s})$,因此只需要研究值函数。
第一行为Bellman方程,可以理解成已知转移概率时的全概率展开。根据算法步骤2,可以得到确定性策略,于是进一步简化为第二行。注意:此处$V^\pi(\mathbf{s})$代表最优策略情况下取得的V函数。在值函数迭代中,V函数均指最优V函数。
值函数迭代法
由A与Q的关系可知$\arg\max_{\mathbf{a}_ t}A^\pi(\mathbf{s}_ t,\mathbf{a}_ t)=\arg\max_{\mathbf{a}_t}Q^\pi(\mathbf{s}_t,\mathbf{a}_t)$,因此可以用Q去替代算法中的A,跳过策略(actor-critic中需要在特定策略下,由r对时间累加得到V,训练拟合V网络;现在由V计算Q,然后最大化得到新的V),得到更简单的值函数迭代法(Value Iteration, VI):
- 更新Q函数:$Q(\mathbf{s},\mathbf{a})=r(\mathbf{s},\mathbf{a})+\gamma\mathbf{E}[V(\mathbf{s}’)]$,普通等式;
- 更新V函数:$V(\mathbf{s})=\max_\mathbf{a}Q(\mathbf{s},\mathbf{a})$,最优策略下V与Q的关系。
算法中只是对V函数迭代,Q函数没有作用。实际使用中,状态个数十分巨大,意味着这种类似于动态规划的算法需要很大的表。因此可以用神经网络代替这个表,即输入状态,输出对应的值函数,损失函数为$\mathcal{L}(\phi)=\frac{1}{2}\left\Vert V_\phi(\mathbf{s})-\max_\mathbf{a}Q^\pi(\mathbf{s},\mathbf{a})\right\Vert^2$,这就是拟合值函数迭代法(Fitted Value Iteration):
- $\mathbf{y}_ i\leftarrow\max_{\mathbf{a}_ i}(r(\mathbf{s}_ i,\mathbf{a}_ i)+\gamma\mathbf{E}[V_\phi(\mathbf{s}_i’)])$
- $\phi\leftarrow\arg\min_\phi\frac{1}{2}\sum_i\left\Vert V_\phi(\mathbf{s}_i)-\mathbf{y}_i\right\Vert^2$
这里面最大的问题是max操作,只有假设状态转移概率已知,并且在$\mathbf{s}_ i$下遍历各种$\mathbf{a}_ i$才能得到$\mathbf{s’}_ i$并求得期望,但有些场景下不可能让你反复尝试来收集数据。如何避免这种情况?已知最优策略下$Q^\pi(\mathbf{s},\mathbf{a})= r(\mathbf{s},\mathbf{a})+\gamma\mathbf{E}_ {\mathbf{s}’\sim p(\mathbf{s}’\vert \mathbf{s},\mathbf{a})}[Q^\pi(\mathbf{s}’,\pi(\mathbf{s}’))]$,意味着有了Q-函数,即使没有转移概率也能运算(不需要max操作,因为当前的Q暗示已经进行过max操作了)。这称为拟合Q函数迭代算法(Fitted Q-Iteration):
- 执行某个策略,收集容量为N的数据集${(\mathbf{s}_i,\mathbf{a}_i,r_i,\mathbf{s}’_i)}$;
- $\mathbf{y}_ i\leftarrow r(\mathbf{s}_ i,\mathbf{a}_ i)+\gamma\mathbf{E}[V_\phi(\mathbf{s}_ i’)]$,其中使用$\max_{\mathbf{a}_ i’}Q_\phi(\mathbf{s}_ i’,\mathbf{a}_ i’)$来近似$\mathbf{E}[V_\phi(\mathbf{s}_ i’)]$(最佳策略下$V(\mathbf{s})=\max_\mathbf{a}Q(\mathbf{s},\mathbf{a})$);
- $\phi\leftarrow\arg\min_\phi\frac{1}{2}\sum_i\left\Vert Q_\phi(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{y}_i\right\Vert^2$。反复执行2-3多次,在回到1执行。
对该算法有几点备注:
- 第2步有max操作,这个是对Q网络进行遍历,不需要已知状态转移概率;
- 第一步可以是任何策略,可以收集一批数据,也可以是一个的在线版本;
- off-policy:$\max_{\mathbf{a}_ i’}Q_\phi(\mathbf{s}_i’,\mathbf{a}_i’)$只是对决策空间的一个枚举,而$r(\mathbf{s}_i,\mathbf{a}_i)$也与策略没关系;
- 只有值函数网络,没有策略梯度,没有高方差问题(算法收集了一大堆数据,而非一条轨迹,从这角度也可以解释);
- 缺点:对非线性函数近似,不确保能收敛;
- 理想情况下,算法最优解对应于最优Q函数的Bellman方程。
在线Q迭代算法(Online Q-iteration):
- 执行某个行动$\mathbf{a}_i$,收集观察数据$(\mathbf{s}_i,\mathbf{a}_i,r_i,\mathbf{s}’_i)$
- $\mathbf{y}_ i\leftarrow r(\mathbf{s}_ i,\mathbf{a}_ i)+\gamma\max_{\mathbf{a}_ i’}Q_\phi(\mathbf{s}_i’,\mathbf{a}_i’)$
- $\phi\leftarrow\phi-\alpha\frac{\mathrm{d} Q_\phi(\mathbf{s}_ i,\mathbf{a}_ i)}{\mathrm{d}\phi}(Q_\phi(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{y}_i)$
该算法每轮执行一个行动,得到一个转移观察,算出目标值,做一步的随机梯度下降。第一步行动的选择最好使用$\epsilon$-贪心或Boltzmann探索,这在以后会讲。
值函数理论(一些大致证明,并不精确)
对于算法$V(\mathbf{s})\leftarrow\max_\mathbf{a}[r(\mathbf{s},\mathbf{a})+\gamma\mathbf{E}[V(\mathbf{s}’)]]$,我们想知道它是否收敛。定义一个算子$\mathcal{B}$,使得$\mathcal{B}V=\max_\mathbf{a}r_\mathbf{a}+\gamma\mathcal{T}_ \mathbf{a}V$,$\mathcal{T}_ \mathbf{a}$指的是选择行动$\mathbf{a}$的转移矩阵。可以证明$V^* $是$\mathcal{B}$算子的一个不动点,因为$V^* (\mathbf{s})=\max_\mathbf{a}[r(\mathbf{s},\mathbf{a})+\gamma\mathbf{E}[V^* (\mathbf{s}’)]]=\mathcal{B}V^*$。这个不动点代表最优策略或最优值函数。
那么是否可以收敛到这个最优点?我们有$\Vert\mathcal{B}V-\mathcal{B}\bar{V}\Vert_\infty\leq\gamma\Vert V-\bar{V}\Vert_\infty$。令$\bar{V}=V^* $,可以有$\Vert\mathcal{B}V-V^* \Vert_\infty\leq\gamma\Vert V-V^* \Vert_\infty$,即操作符每作用一次值函数,离最佳值函数就会更进一步。拟合值函数迭代算法中,有限的神经网络只能表示值函数的一个子集,如图中的蓝色直线。算法中我们从一个函数出发,进行一次$\mathcal{B}$操作,使用最小二乘回归来投影到这个函数集合。
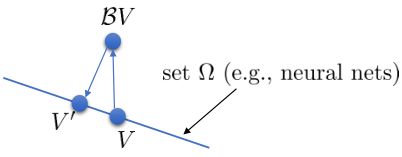
我们定义投影算子$\Pi V=\arg\min_{V’\in\Omega}\frac{1}{2}\sum\Vert V’(\mathbf{s})-V(\mathbf{s})\Vert^2$,则算法可以写成$V\leftarrow\Pi\mathcal{B}V$这样的复合映射。注意$\mathcal{B}$是一个无穷模下的收缩映射,$\Pi$是一个2模下的收缩映射,但问题在于如果我们将这两个映射进行复合,那么$\Pi\mathcal{B}$并不是一个收缩映射,因为它们不是在同一个模下收缩的。
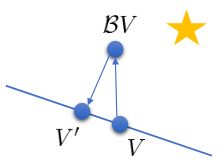
不用无穷模的原因是当状态空间很大的情况下,无穷模下的投影问题极其难解,只能寻求找到最优解的一个投影,但是事与愿违的是。因此我们的结论是,值函数迭代法在表格中是收敛的,但是拟合值函数迭代法在一般意义下是不收敛的,在实践中也通常不收敛,但是有一些方法来缓解这些问题。
总结
- 引入:policy gradient和actor-critic都是利用策略梯度进行优化,也可以使用策略迭代法(完全抛弃策略这一概念):1. 计算$A^\pi(\mathbf{s}_t,\mathbf{a}_t)$;2. 选择使$A^\pi(\mathbf{s}_t,\mathbf{a}_t)$最大的$a_t$作为策略$\pi(\mathbf{a}_t\vert\mathbf{s}_t)$。
- 拟合值函数迭代法,拟合Q函数迭代法
- 拟合值函数迭代法需要已知状态转移概率来遍历所有状态,拟合Q函数迭代法不需要
- off-policy,采集数据时与策略无关
- 没有策略梯度,没有高方差问题
- 收敛性不确定
- 不收敛性:可以证明值函数迭代法在无穷模下是收敛的(表格法),不保证在2模下收敛(在深度学习中使用欧氏距离迭代);算法中的梯度不是对目标函数的梯度,因此也并不是梯度下降法