Q-函数:$Q^\pi(\mathbf{s}_ t,\mathbf{a}_ t)=\sum_{t’=t}^T\mathbf{E}_ {\pi_\theta}[r(\mathbf{s}_ {t’},\mathbf{a}_ {t’}) \vert \mathbf{s}_ t,\mathbf{a}_ t]$
V-值函数:$V^{\pi}(\mathbf{s}_ t)=\sum_{t’=t}^T\mathbf{E}_ {\pi_\theta}[r(\mathbf{s}_ {t’},\mathbf{a}_{t’})\vert \mathbf{s}_t]$
关系:$V^\pi(\mathbf{s}_ t)=\mathbf{E}_ {\mathbf{a}_ t\sim\pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)}[Q^\pi(\mathbf{s}_t,\mathbf{a}_t)]$
优势函数(advantage function):$A^\pi(\mathbf{s}_t,\mathbf{a}_t)=Q^\pi(\mathbf{s}_t,\mathbf{a}_t)-V^\pi(\mathbf{s}_t)$
由上一讲提到的今后收益$\hat{Q}_ {i,t}=\sum_{t’=t}^Tr(\mathbf{s}_ {i,t’},\mathbf{a}_ {i,t’}) \approx\sum_{t’=t}^T\mathbf{E}_ {\pi_\theta}[r(\mathbf{s}_ {t’},\mathbf{a}_{t’})\vert \mathbf{s}_t,\mathbf{a}_t]$与Q-函数相对应,但是这个收益只是由一条路径计算得到的,同一分布的轨迹也可能差别很大,因此具有高方差性。这个近似是导致策略梯度法无法快速收敛的原因。同样,上一讲提到的baseline常数与V-函数相对应,表示给定策略下Q-函数的期望。
针对这个问题,我们期望引入神经网络,因为神经网络高偏差(拟合不准确)低方差。这种偏差-方差的权衡很常见。
Actor-Critic算法
它与策略梯度法在第一步生成样本和第三步策略改进上并没有显著区别,主要区别在于第二步:我们现在尝试去做的是去拟合一个值函数:$Q^\pi,V^\pi,A^\pi$三者之一(通常是$V^\pi$,因为它只依赖于$s_t$,状态空间小,方差小),以期能得到一个更好的梯度估计。我们真正从“估计收益”变为了“拟合模型”。
对Q-函数做变形:
其中,第一行提取当前收益,因为给定当前状态和行动,当前收益就已经确定。第三行采用近似,使用一步以后的状态近似整条轨迹,这里会引入一些精度损失。这样,优势函数就可以近似为
这样,只需要训练网络参数$\phi$,输入状态$\mathbf{s}$,输出估计量$\hat{V}^\pi(\mathbf{s})$。而且,不需要对未来所有值累加,只需要知道下一状态。
给定一个策略去拟合这样一个神经网络的过程我们称为策略评估 (Policy Evaluation)。这个步骤只是从任意给定的状态出发,评估当前策略有多好,而并不去改进策略。由于目标函数$J(\theta)=\mathbf{E}_ {\mathbf{s}_ 1\sim p(\mathbf{s}_ 1)}[V^\pi(\mathbf{s}_ 1)]$只是值函数的一个期望而已,所以拟合V-值函数也为我们带来了目标函数。具体做法是我们依然使用蒙特卡洛方法,进行一次轨迹采样以后来近似$V^\pi(\mathbf{s}_ t)\approx\sum_{t’=t}^Tr(\mathbf{s}_ {t’},\mathbf{a}_{t’})$。当然如果我们可以重启模拟器的话,最好能做多次轨迹采样,但是前者其实也还是不错的。
目标函数可以重写为另一种形式:
第二个约等号表示将值函数用已经训练的神经网络的结果代替,这相当于自助法(bootstrap)。虽然神经网络会产生一些偏差,比如我们从比较接近的两个状态出发做两条轨迹,结果上可能会有很大差别,但对于神经网络,它会拟合多个样本,并将其综合到一个低方差版本。这种情况下,网络会对两条轨迹做平均。如果两状态间存在断崖,网络答案就会出现问题。但不管怎么说,使方差减小总是好的。因此这个表达式的变换的意义在于增大偏差较小方差。
Batch Actor-Critic具体算法:
- 运行机器人,根据策略$\pi_\theta(\mathbf{a}\vert \mathbf{s})$得到整个轨迹的一些样本$\lbrace\mathbf{s}_i,\mathbf{a}_i\rbrace$,包括所处状态、行动和收益。
- 使用样本$\left\lbrace\left(\mathbf{s}_ {i,t},y_{i,t}:=\sum_{t’=t}^T r(\mathbf{s}_ {i,t},\mathbf{a}_ {i,t})\right)\right\rbrace$拟合$\hat{V}^\pi_\phi(\mathbf{s})$(最小二乘法)。这一步样本可以做蒙特卡洛,也可以做自助法。
- 评估优势函数$\hat{A}^\pi(\mathbf{s}_ i,\mathbf{a}_ i)=r(\mathbf{s}_ i,\mathbf{a}_ i)+\hat{V}^\pi_\phi(\mathbf{s}_ i’)-\hat{V}^\pi_\phi(\mathbf{s}_i)$。
- 放入策略梯度函数$\nabla_\theta J(\theta)\approx\sum_{t=1}^T\left[\nabla_\theta\log \pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)\hat{A}^\pi(\mathbf{s}_t,\mathbf{a}_t)\right]$。
- 走一个梯度步$\theta\leftarrow \theta+\alpha\nabla_\theta J(\theta)$。
discount factor
对于无限长序列,累加可能会使目标函数值越来越大,因此引入折扣因子(discount factor)的概念,希望收益发生的时间更接近现在,表达式修改成$y_{i,t}\approx r(\mathbf{s}_ {i,t},\mathbf{a}_ {i,t})+\gamma\hat{V}_ \phi^\pi(\mathbf{s}_{i,t+1})$。实际情况中设成0.99。
在策略梯度法中引入折扣因子有两种方式。第一种,对利用因果关系后的表达式进行修改,
第二种,对一开始的策略梯度表达式修改,
两种方法略有区别。第二种方法从时间点1开始加折扣因子,但通常人们使用第一种方法,因为人们不关心一开始,而只关心当前。
对Actor-Critic算法,只需要将第三步$\hat{A}^\pi(\mathbf{s}_ i,\mathbf{a}_ i)=r(\mathbf{s}_ i,\mathbf{a}_ i)+\hat{V}^\pi_\phi(\mathbf{s}_ i’)-\hat{V}^\pi_\phi(\mathbf{s}_ i)$改成$\hat{A}^\pi(\mathbf{s}_ i,\mathbf{a}_ i)=r(\mathbf{s}_ i,\mathbf{a}_ i)+\gamma\hat{V}^\pi_\phi(\mathbf{s}_ i’)-\hat{V}^\pi_\phi(\mathbf{s}_i)$即可。
online Actor-Critic具体算法(加粗的表示与batch Actor-Critic的区别)。由于是在线的,因此每一步均使用一个样本进行更新:
- 运行机器人,根据策略$\pi_\theta(\mathbf{a}\vert \mathbf{s})$得到一个状态转移样本$(\mathbf{s},\mathbf{a},\mathbf{s}’,r)$,不需要整条轨迹。
- 使用用$r+\gamma\hat{V}^\pi_\phi(\mathbf{s}’)$来更新$\hat{V}^\pi_\phi(\mathbf{s})$。(类似于自助法)
- 评估优势函数$\hat{A}^\pi(\mathbf{s}_ i,\mathbf{a}_ i)=r(\mathbf{s}_ i,\mathbf{a}_ i)+\hat{V}^\pi_\phi(\mathbf{s}_ i’)-\hat{V}^\pi_\phi(\mathbf{s}_i)$。
- 放入策略梯度函数$\nabla_\theta J(\theta)\approx\sum_{t=1}^T\left[\nabla_\theta\log \pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)\hat{A}^\pi(\mathbf{s}_t,\mathbf{a}_t)\right]$。
- 走一个梯度步$\theta\leftarrow \theta+\alpha\nabla_\theta J(\theta)$。
可惜的是,如果用神经网络,单纯这样做online版本算法并没有用,除非用到下面的实现细节。
实现细节
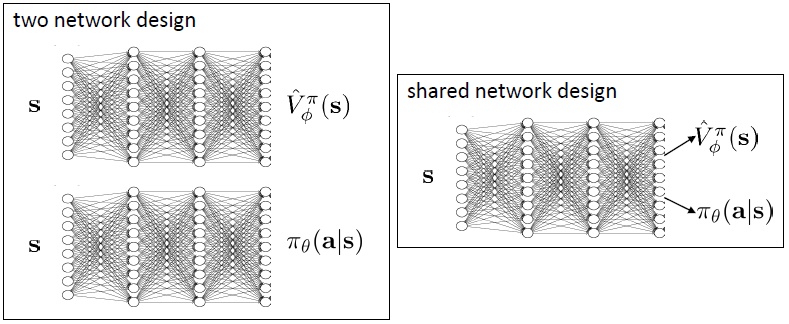
需要两个神经网络,一个从状态$\mathbf{s}$映射到演员策略$\pi_\theta(\mathbf{a}\vert \mathbf{s})$,另一个从状态$\mathbf{s}$映射到$\hat{V}^\pi_\phi(\mathbf{s})$。如果两个网络相互独立,训练会更加稳定,但不能很好地利用特征。
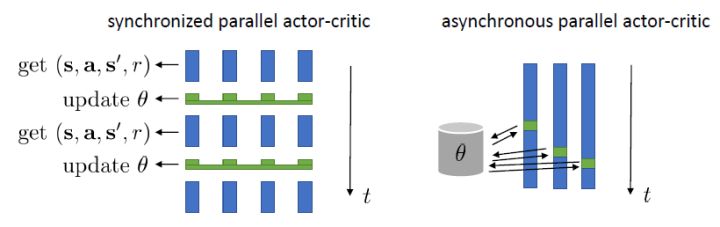
online Actor-Critic是属于on-policy算法,意味着每次更新参数后需要重新采样数据,这样每次只有一个样本(并不适合网络的训练)。如何把它做成批量形式。一种是采用同步并行,用多个智能体同时采数据,缺点是每一步结束之后需要强制同步。另一种是异步并行,每个智能体完成操作后将梯度传回中央服务器,中央服务器在累计一定的步数后,将更新信息传回智能体。第二种方法更实用。
不同baselines
综合看目标函数的梯度表达式,
第一行是Actor-Critic算法,critic函数使得方差变小,但由于critic函数不能被完全拟合(训练初期网络结果肯定是错的),因此会有偏差;第二行是policy gradient算法,由于蒙特卡洛抽样,是无偏的,但是单样本估计使得方差很高;第三行是结合的算法,它只改变与$\mathbf{s}_ {i,t}$相关的函数,依然是无偏的,同时基准线依赖于状态,更接近真实收益,因此方差相对会小。如果使用$\mathbf{a}_ {i,t}$相关的baseline,不在是无偏的,但依然能用,如下:
它加入了修正项使其无偏,并且如果修正项可以被评估,它就能使用。这会在后续讲到????可以得到的结论是:基于状态的基准线是无偏的,基于行动的基准线是有偏的,但是偏差有可能可以通过一个校正项补救回来。
n步收益
无论是Actor-Critic还是纯粹的MC算法,其缺点都是明显的,有没有折中的办法。可以预见的是,随着轨迹增加,收益会减小,方差会变大,因此可以在前期使用MC算法,后期使用Actor-Critic算法,即:
这又称为n步收益,通常n为5。广义优势估计(Generalized Advantage Estimation, GAE)是对n步收益的推广,它不再选择一个单一的步数,而是对所有的步数进行一个加权平均,
$\lambda$非常像一个折扣因子,如果它比较小,那么我们将在很早期就切断,偏差较大方差较小;反之则较后切断,偏差较小方差较大。因此从另一种意义上解读,折扣因子意味着方差降低。
总结
- 引入:因果关系policy gradient引入了Q函数,但这个Q函数只使用一个样本,因此高方差。希望用神经网络(低方差)代替Q函数,以权衡偏差-方差问题。
- 思路:
- 类似baseline机制,将Q函数转化成A函数
- 由于V函数状态空间小,因此改写成V函数的表达式
- 利用单步近似整条轨迹(引入偏差)
- 算法:比policy-gradient多一步,即用$\left\lbrace\left(\mathbf{s}_ {i,t},y_{i,t}:=\sum_{t’=t}^T r(\mathbf{s}_ {i,t},\mathbf{a}_ {i,t})\right)\right\rbrace$训练值函数网络$\hat{V}^\pi_\phi(\mathbf{s})$。
- discount factor:针对无限长问题
- batch版本需要采样多个样本整条轨迹计算V函数,online版本只需一个样本一个转移状态利用$V(s_{t+1})$更新$V(s_t)$
- actor-critic与MC采样:actor-critic高偏差(不能完全拟合)低方差,MC采样相反。因此可以前期使用MC,后期使用actor-critic