DQN的引入
我们从在线Q迭代算法入手,它包含三个步骤:
- 执行某个行动$\mathbf{a}_i$,收集观察数据$(\mathbf{s}_i,\mathbf{a}_i,r_i,\mathbf{s}’_i)$
- $\mathbf{y}_ i\leftarrow r(\mathbf{s}_ i,\mathbf{a}_ i)+\gamma\max_{\mathbf{a}_ i’}Q_\phi(\mathbf{s}_i’,\mathbf{a}_i’)$
- $\phi\leftarrow\phi-\alpha\frac{\mathrm{d} Q_\phi(\mathbf{s}_ i,\mathbf{a}_ i)}{\mathrm{d}\phi}(Q_\phi(\mathbf{s}_i,\mathbf{a}_i)-\mathbf{y}_i)$
这个算法有两个问题:序列状态的强相关性,以及目标值总在变动。
问题一:序列状态的强相关性
序列样本为什么会成为问题?考虑正弦波的回归问题,我们一般希望采样的样本是独立同分布的,然而序列样本有先后问题,这样很容易在局部形成过拟合,忘掉其他信息。一种解决办法是类似actor-critic,使用多个智能体同时收集数据,并行计算,减小样本相关度。另一种方法更常见,即回放缓冲池(Replay Buffer),这是Q-learning这种off-policy算法所特有的。具体方法是先使用任意策略收集大量样本,然后从样本池中随机选取进行梯度更新,同时需要使用探索策略向样本池输入新样本。注意到,如果缓冲区足够大的话,那么新进入数据占权重其实是很小的,很可能不会被抽到。当然这不是个问题,新进数据只是为了让样本池的支撑集更广。

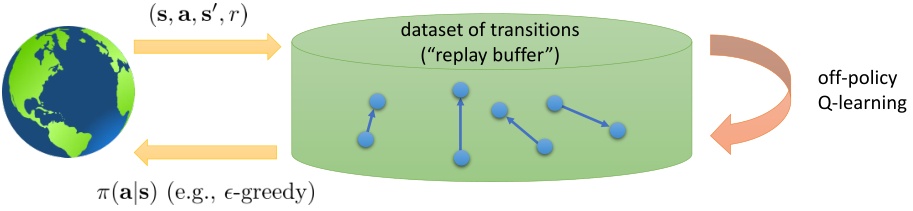
问题二:目标值总在变动
我们想要使得$Q_\phi(\mathbf{s}_ i,\mathbf{a}_ i)$尽量靠近目标值$r(\mathbf{s}_ i,\mathbf{a}_ i)+\gamma\max_{\mathbf{a}_ i’}Q_\phi(\mathbf{s}_ i’,\mathbf{a}_ i’)$,但不停迭代$Q_\phi(\mathbf{s}_i,\mathbf{a}_i)$会使目标值一直变动。解决思路是,先把目标值算出来,然后再去做最小化最小二乘的回归,那么这样的回归就会稳定很多。具体做法是,先执行若干步(如10000步)整个算法迭代,然后把网络的参数$\phi$存下来称为目标网络$\phi’$,这样梯度更新变成了:
DQN算法
目标函数变成了$Q_{\phi’}$而不是$Q_{\phi}$。这样目标函数会在一段时间内固定,变成了一个监督学习算法。综合以上两种技巧,就是举世闻名的DQN算法(Deep Q Network):
- 在环境中执行某个操作$\mathbf{a}_i$,观察到$(\mathbf{s}_i,\mathbf{a}_i,r_i,\mathbf{s}’_i)$,并加入到回放缓冲池$\mathcal{B}$中。
- 均匀地从回放缓冲池$\mathcal{B}$中抽取一个小批量样本$\lbrace(\mathbf{s}_j,\mathbf{a}_j,r_j,\mathbf{s}’_j)\rbrace$。
- 使用目标网络$Q_{\phi’}$,计算出目标值$y_j=r_j+\gamma\max_{\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_j’,\mathbf{a}_j’)$。
- 走一个梯度步,$\phi\leftarrow\phi-\alpha\sum_j\frac{\mathrm{d} Q_\phi(\mathbf{s}_ j,\mathbf{a}_ j)}{\mathrm{d}\phi}\left(Q_\phi(\mathbf{s}_j,\mathbf{a}_j)-y_j\right)$。
- 每隔N步,把整个神经网络的参数$\phi$复制到目标网络$\phi’$中去。返回第一步。
其中,3、4可以并行。

当目标网络更新后,之后一系列步骤都将以它为基准进行更新。这些步骤中后面的步骤误差比较大,可以使用一个类似于指数平滑的方法,不再是若干步执行更新,而是每一步都做一个小变动。因此第5步改成:$\phi’\leftarrow\tau\phi’+(1-\tau)\phi$,其中$\tau=0.999$,这称为Polyak Averaging。

让Q-learning更精确
思考的问题是:实验得到的Q值是否能很好的表现未来收益?
max噪声
实验中发现,Q值会比期望收益高出很多(没关系,只需要估计的$Q(\mathbf{s},\mathbf{a}_ 1)-Q(\mathbf{s},\mathbf{a}_ 2)$和真实值差不多就可以工作),原因在于目标值$y_j=r_j+\gamma\max_{\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_ j’,\mathbf{a}_ j’)$的max操作。考虑两个随机变量$X_1$和$X_2$,有$\mathbf{E}[\max(X_1,X_2)]\geq\max(\mathbf{E}[X_1],\mathbf{E}[X_2])$。如果变量含有噪音,取max会使噪音变大,而Q都是从样本轨迹里学出来的,肯定含有噪音。由于$\max_{\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_ j’,\mathbf{a}_ j’)=Q_{\phi’}(\mathbf{s}_ j’,\arg\max_{\mathbf{a}’}Q_{\phi’}(\mathbf{s}’,\mathbf{a}’))$,某一行动的Q值过大,操作就会过高估计接下来的行动值,并继续向后传播。
双重Q学习(Double Q-learning)用于缓解这一问题。它使用两个网络$\phi_A$和$\phi_B$,更新时候采用以下交错手段:
也就是说,更新一个网络的时候,使用另一个网络的值,这样就切断了“过高估计的行动-过高估计的值传导”这样的一个链条。在实际中,我们在前面已经介绍了目标网络$\phi’$,可以直接利用它作为另一个网络,由当前网络决定最佳行动:
当前收益与未来收益占比
对于目标值$y_{j,t}=r_{j,t}+\gamma\max_{\mathbf{a}_ {j,t+1}}Q_{\phi’}(\mathbf{s}_ {j,t+1},\mathbf{a}_{j,t+1})$,包含当前收益与未来期望收益。在早期,Q只是噪音,而到后期占比就变大。因此使用N步收益后再把未来的自助项加进去,即:
在早期Q值不准确时可以减少偏差,并有效提升速度。缺点是只支持on-policy策略。之前的表达式只考虑一步转移,与策略无关,因此是off-policy,而现在进行N步转移,必须要求on-oplicy。怎么处理这一问题?第一种,直接忽略,实际中效果还不错。另一种是切割轨迹,把之前的片段拿过来,如果不符合策略,就直接切断。当数据主要是on-policy(需要及时淘汰旧数据)且行动空间很小时效果不错。
连续行动空间的Q-learning
对于目标值$y_j=r_j+\gamma\max_{\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_j’,\mathbf{a}_j’)$,如果行动空间离散,只需要遍历即可,但如果连续,就很麻烦,尤其是这一步位于循环里面。
第一种方法是直接做优化。离散随机踩点$\max_\mathbf{a}Q(\mathbf{s},\mathbf{a})\approx\max\lbrace Q(\mathbf{s},\mathbf{a}_1),\ldots,Q(\mathbf{s},\mathbf{a}_N)\rbrace$,其中行动是从某些分布(如均匀分布)中得到。这样简单、可以并行,在低维时准确率不差。其他一些方法,如交叉熵方法这样的迭代随机优化算法,或者如CMA-ES (Covariance Matrix Adaptation Evolutionary Strategies) 这样的进化算法。
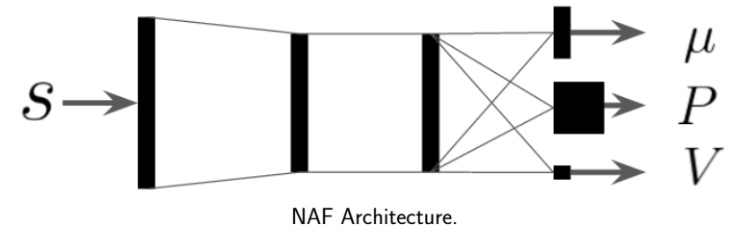
第二种方法是选取一个比较容易优化的函数簇来拟合我们的Q函数。在此之前,我们使用的都是通用的神经网络,有些情况下我们不必要这么做。当Q函数是二次函数的时候$Q_\phi(\mathbf{s},\mathbf{a})=-\frac{1}{2}(\mathbf{a}-\mu_\phi(\mathbf{s}))^\top P_\phi(\mathbf{s})(\mathbf{a}-\mu_\phi(\mathbf{s}))+V_\phi(\mathbf{s})$,我们就训练一个神经网络,输入状态,输出$(\mu,P,V)$,其中$\mu$和$V$都是向量,$P$是矩阵。这样的方法称为NAF(Normalized Advantage Functions),它的天然特性就是$\mu_\phi(\mathbf{s})=\arg\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})$和$V_\phi(\mathbf{s})=\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})$。这样算法上修改简单,缺点是Q只能有固定形式,建模能力受限。
第三种方法更为广泛,是去新学习一个最大化器,被称为DDPG(Deep Deterministic Policy Gradient)。考虑到$\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})=Q_\phi\left(\mathbf{s},\arg\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})\right)$,可以想的是另外训练一个最大化器$\mu_\theta(\mathbf{s})\approx\arg\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})$作为最大化的算子,训练的方法是让$\theta\leftarrow\arg\max_\theta Q_\phi(\mathbf{s},\mu_\theta(\mathbf{s}))$,这个可以用梯度上升法。整个DDPG算法迭代步骤:
- 在环境中执行某个操作$\mathbf{a}_i$,观察到$(\mathbf{s}_i,\mathbf{a}_i,r_i,\mathbf{s}’_i)$,并加入到回放缓冲池$\mathcal{B}$中;
- 均匀地从回放缓冲池$\mathcal{B}$中抽取一个小批量样本$\lbrace(\mathbf{s}_j,\mathbf{a}_j,r_j,\mathbf{s}’_j)\rbrace$;
- 使用目标网络$Q_{\phi’}$和最大化器$\mu_{\theta’}$,计算出目标值$y_j=r_j+\gamma\max_{\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_ j’,\mu_{\theta’}(\mathbf{s}_j’))$;
- 当前网络走一个梯度步,$\phi\leftarrow\phi-\alpha\sum_j\frac{\mathrm{d} Q_\phi(\mathbf{s}_ j,\mathbf{a}_ j)}{\mathrm{d}\phi}\left(Q_\phi(\mathbf{s}_j,\mathbf{a}_j)-y_j\right)$;
- 最大化器走一个梯度步,$\theta\leftarrow\theta+\beta\sum_j\frac{\mathrm{d}\mu(\mathbf{s}_j)}{\mathrm{d}\theta}\frac{\mathrm{d}Q(\mathbf{s}_j,\mathbf{a})}{\mathrm{d}\mathbf{a}}$;
- 使用Polyak Averaging更新$\phi’$和$\theta’$。
DQN的一些技巧
- 很难让Q值稳定,因此建议现在简单情况下(Pong,Breakout)实验程序
- 增加replay buffer
- 收敛慢
- 使用$\epsilon$贪心时,开始的探索率调高,后期减小
- Bellman误差较大,可以对梯度裁剪,或者用Huber损失光滑
- 双重Q很有效
- N步收益不一定有效
- 学习率难调,可以尝试ADAM
- 随机数种子不同,可能导致程序差异很大
总结
- DQN的引入
- 存在两个问题:序列状态的强相关性;目标值总在变动
- 解决方法:replay buffer;固定网络参数进行梯度更新,一段时间后梯度作用于网络
- DQN的问题:
- Q函数高估了实际收益值(max操作导致):两个网络互相迭代,A网络计算梯度作用于B网络
- 回归的目标值中,到后期Q值占比比较高:N步收益+未来收益
- 连续空间:DQN存在max操作,对于连续值很复杂
- DDPG:$\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})=Q_\phi\left(\mathbf{s},\arg\max_\mathbf{a}Q_\phi(\mathbf{s},\mathbf{a})\right)$,训练最大化网络得到a。