CS294 L05 Policy Gradients Introduction

• Policy Gradients
  • 1. 推导
    • 与极大似然估计
    • 部分观测信息
  • 2. 算法存在的问题
    • 问题一：高方差问题
      • 解决方法一：因果关系
      • 解决方法二：基准线（baseline）
    • 问题二：natural gradient
  • 3. 离线的策略梯度法
  • 4. 用自动求导做策略梯度法
• 总结

Policy Gradients

1. 推导

已知轨迹出现的概率$p_\theta(\tau)=p(\mathbf{s}_ 1)\prod_{t=1}^T\pi_\theta(\mathbf{a}_ t|\mathbf{s}_ t)p(\mathbf{s}_{t+1}|\mathbf{s}_t,\mathbf{a}_t)$，目标函数为：

$$J(\theta)=\mathbf{E}_{\tau\sim p_\theta(\tau)}\left[\sum_tr(\mathbf{s}_t,\mathbf{a}_t)\right]$$

如果分布很复杂，通常采用蒙特卡洛法抽样近似。现在考虑如何改进策略。最常见的方式是优化梯度：

$$\begin{align} \nabla_\theta J(\theta) &= \nabla_\theta \mathbf{E}_{\tau\sim p_\theta(\tau)}[r(\tau)] \\ &= \int \nabla_\theta p_\theta(\tau)r(\tau)\mathrm{d}\tau \\ &= \int p_\theta(\tau)\nabla_\theta \log p_\theta(\tau)r(\tau)\mathrm{d}\tau \\ &= \mathbf{E}_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log p_\theta(\tau)r(\tau)] \\ &= \mathbf{E}_{\tau\sim p_\theta(\tau)}\left[\left(\sum_{t=1}^T\nabla_\theta\log \pi_\theta(\mathbf{a}_t|\mathbf{s}_t)\right)\left(\sum_{t=1}^Tr(\mathbf{s}_t,\mathbf{a}_t)\right)\right] \end{align}$$

这个表达式的优点是：我们不需要初始状态以及转移概率，即我们可以在任意环境中直接进行抽样生成样本。接下来可以采用蒙特卡洛估计方法，流程如下：

1. 运行策略$\pi_\theta(\mathbf{a}\vert \mathbf{s})$，抽取样本${\tau^i}$；
2. 计算目标函数，估计梯度$\nabla_\theta J(\theta)\approx\frac{1}{N}\sum_{i=1}^N\left[\left(\sum_{t=1}^T\nabla_\theta\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{s}_ {i,t})\right)\left(\sum_{t=1}^Tr(\mathbf{s}_ {i,t},\mathbf{a}_{i,t})\right)\right]$；
3. 梯度上升$\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$。 这里的$\nabla_\theta\log \pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)$与策略分布相关，如果策略网络的输出是一个高斯分布的均值-方差，那么该表达式在梯度更新时就是对高斯分布求导。

与极大似然估计

策略梯度和极大似然估计（梯度是$\nabla_\theta J_\mathrm{ML}(\theta)\approx\frac{1}{N}\sum_{i=1}^N\nabla_\theta \log p_\theta(\tau_i)$）很类似，区别在于策略梯度法尝试对不同的样本进行加权（reward函数），减少一些不好的样本的出现概率，增加其他样本的出现概率，而极大似然是增加所有样本的出现概率。

部分观测信息

如果只有部分观测信息，依然可以使用策略梯度法。注意，此时等式变成（$o_{i,t}$代替$s_{i,t}$）

$$\nabla_\theta J(\theta)\approx\frac{1}{N}\sum_{i=1}^N\left[\left(\sum_{t=1}^T\nabla_\theta\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{o}_ {i,t})\right)\left(\sum_{t=1}^Tr(\mathbf{o}_ {i,t},\mathbf{a}_{i,t})\right)\right]$$

注意策略梯度的推导过程中转移概率不起作用，因此算法不需要具备马尔可夫性，其他算法不能这么使用。通常不能保证得到一个很好的策略，但能在策略簇中找到一个不错的策略。

2. 算法存在的问题

问题一：高方差问题

理论上，收益值（一个期望）加上一个常数不会影响实际策略。然而，在采样有限的情况下，实际策略会因此而改变，这是因为有限采样造成的高方差。

解决方法一：因果关系

$$\begin{align} \nabla_\theta J(\theta) &\approx \frac{1}{N}\sum_{i=1}^N\left[\left(\sum_{t=1}^T\nabla_\theta\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{s}_ {i,t})\right)\left(\sum_{t=1}^Tr(\mathbf{s}_ {i,t},\mathbf{a}_{i,t})\right) \right] \\ &\approx \frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\left[\nabla_\theta\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{s}_ {i,t})\left(\sum_{t'=t}^Tr(\mathbf{s}_ {i,t'},\mathbf{a}_{i,t'})\right)\right] \end{align}$$

我们把$\hat{Q}_ {i,t}=\sum_{t’=t}^Tr(\mathbf{s}_ {i,t’},\mathbf{a}_{i,t’})$记作今后收益（reward-to-go），这是因为当前策略只会影响之后收益。这样做，累加和的个数减少了，方差也随之减小（因为更接近真实情况）。

解决方法二：基准线（baseline）

对于$\nabla_\theta J(\theta)=\mathbf{E}_ {\tau\sim p_\theta(\tau)}[\nabla_\theta \log p_\theta(\tau)r(\tau)]$，正如之前所述，采样的有限性导致表达式对收益值很敏感。因此我们不想考察轨迹自身有多好，而是它比平均好多少，可以修改为$\nabla_\theta J(\theta)=\mathbf{E}_ {\tau\sim p_\theta(\tau)}[\nabla_\theta \log p_\theta(\tau)(r(\tau)-b)]$。有限采样时，常数不影响期望，却影响方差。如何选取一个理论上最优的常数？只要使得方差最小即可。将表达式带入方差公式$\text{Var}[X]=\mathbf{E}[X^2]-\mathbf{E}[X]^2$并对b求导数，令$g(\tau):=\nabla_\theta \log p_\theta(\tau)$，得到最优常数$b^*=\frac{\mathbf{E}[g(\tau)^2 r(\tau)]}{\mathbf{E}[g(\tau)^2]}$。这个常数计算比较复杂，不如直接使用收益值的期望。（注：此处证明了存在最佳常数baseline，下一讲会介绍最佳baseline是与state相关的）

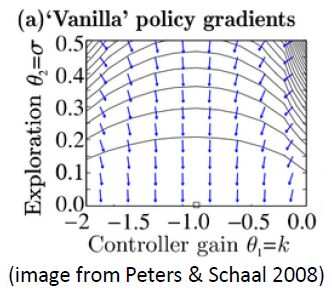
问题二：natural gradient

假设对数策略函数是一个高斯分布，形式是$\log\pi_\theta(\mathbf{a}_t|\mathbf{s}_t)=-\frac{1}{2\sigma^2}(k\mathbf{s}_t-\mathbf{a}_t)^2+\text{const}$，收益函数$r(\mathbf{s}_t,\mathbf{a}_t)=-\mathbf{s}_t^2-\mathbf{a}_t^2$。使用策略梯度法时，梯度法总会倾向于减小$\sigma$，更小的$\sigma$，更倾向于让我们进一步减少$\sigma$，导致$\sigma$会快速下降，然后逐渐地$k$就不动了。

3. 离线的策略梯度法

策略梯度法是on-policy算法，因为表达式中$\nabla_\theta J(\theta)=\mathbf{E}_ {\tau\sim p_\theta(\tau)}[\nabla_\theta \log p_\theta(\tau)r(\tau)]$求期望时需要从当前分布上进行采样，意味着每次网络更新后都需要重新采样，训练会非常慢。假设有一堆从分布$\hat{p}(\tau)$中采样的数据，如何用这些数据去估计。

重要性采样（importance sampling）： $\mathbf{E}_ {x\sim p(x)}[f(x)]=\int p(x)f(x)\mathrm{d}x=\int q(x)\frac{p(x)}{q(x)}f(x)\mathrm{d}x=\mathbf{E}_ {x\sim q(x)}\left[\frac{p(x)}{q(x)}f(x)\right]$

新的目标函数变成$J(\theta)=\mathbf{E}_ {\tau\sim \hat{p}(\tau)}\left[\frac{p_\theta(\tau)}{\hat{p}(\tau)}r(\tau)\right]$，其中$\frac{p_\theta(\tau)}{\hat{p}(\tau)}=\frac{p(\mathbf{s}_ 1)\prod_{t=1}^T\pi_\theta(\mathbf{a}_ t\vert \mathbf{s}_ t)p(\mathbf{s}_ {t+1}\vert \mathbf{s}_ t,\mathbf{a}_ t)}{p(\mathbf{s}_ 1)\prod_{t=1}^T\hat{\pi}(\mathbf{a}_ t\vert \mathbf{s}_ t)p(\mathbf{s}_ {t+1}\vert \mathbf{s}_ t,\mathbf{a}_ t)}=\frac{\prod_{t=1}^T\pi_\theta(\mathbf{a}_ t\vert \mathbf{s}_ t)}{\prod_{t=1}^T\hat{\pi}(\mathbf{a}_ t\vert \mathbf{s}_ t)}$。对于新参数$\theta’$，$J(\theta’)=\mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\frac{p_{\theta’}(\tau)}{p_{\theta}(\tau)}r(\tau)\right]$，于是梯度更新公式变成：

$$\begin{align} \nabla_{\theta'}J(\theta') &= \mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\frac{\nabla_{\theta'}p_{\theta'}(\tau)}{p_{\theta}(\tau)}r(\tau)\right] \\ &= \mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\frac{p_{\theta'}(\tau)}{p_{\theta}(\tau)}\nabla_{\theta'}\log p_{\theta'}(\tau)r(\tau)\right] \\ &= \mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\left(\prod_{t=1}^T\frac{\pi_{\theta'}(\mathbf{a}_ t\vert \mathbf{s}_ t)}{\pi_{\theta}(\mathbf{a}_ t\vert \mathbf{s}_ t)}\right)\left(\sum_{t=1}^T\nabla_{\theta'}\log \pi_{\theta'}(\mathbf{a}_ t\vert \mathbf{s}_ t)\right)\left(\sum_{t=1}^Tr(\mathbf{s}_t,\mathbf{a}_t)\right)\right] \\ &= \mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\sum_{t=1}^T\nabla_{\theta'}\log \pi_{\theta'}(\mathbf{a}_ t\vert \mathbf{s}_ t)\left(\prod_{t'=1}^t\frac{\pi_{\theta'}(\mathbf{a}_ {t'}\vert \mathbf{s}_ {t'})}{\pi_{\theta}(\mathbf{a}_ {t'}\vert \mathbf{s}_ {t'})}\right)\left(\sum_{t'=t}^Tr(\mathbf{s}_ {t'},\mathbf{a}_ {t'})\left(\prod_{t''=t}^{t'}\frac{\pi_{\theta'}(\mathbf{a}_ {t''}\vert \mathbf{s}_ {t''})}{\pi_{\theta}(\mathbf{a}_ {t''}\vert \mathbf{s}_ {t''})}\right)\right)\right] \end{align}$$

最后一步假如因果关系进行修正。如果忽略最后一项连乘，就是策略迭代法，以后会讲？？？？这部分存在新问题，即中间的连乘部分会导致值过小的问题，解决办法是将目标函数写成边际分布情况下求期望的形式：

$$\begin{align} J(\theta) &= \sum_{t=1}^T\mathbf{E}_ {(\mathbf{s}_ t,\mathbf{a}_ t)\sim p_\theta(\mathbf{s}_t,\mathbf{a}_t)}[r(\mathbf{s}_t,\mathbf{a}_t)] \\ &= \sum_{t=1}^T\mathbf{E}_ {\mathbf{s}_ t\sim p_\theta(\mathbf{s}_ t)}\left[\mathbf{E}_ {\mathbf{a}_ t\sim\pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)}[r(\mathbf{s}_t,\mathbf{a}_t)]\right] \end{align}$$

这样可以在两个层面上做重要性抽样了：

$$J(\theta')=\sum_{t=1}^T\mathbf{E}_ {\mathbf{s}_ t\sim p_\theta(\mathbf{s}_ t)}\left[\frac{p_{\theta'}(\mathbf{s}_ t)}{p_{\theta}(\mathbf{s}_ t)}\mathbf{E}_ {\mathbf{a}_ t\sim\pi_\theta(\mathbf{a}_ t\vert \mathbf{s}_ t)}\left[\frac{\pi_{\theta'}(\mathbf{a}_ t\vert \mathbf{s}_ t)}{\pi_{\theta}(\mathbf{a}_t\vert \mathbf{s}_t)}r(\mathbf{s}_t,\mathbf{a}_t)\right]\right]$$

但这样又碰到新问题，即$p_{\theta’}(\mathbf{s}_ t)$无法求解。通常省略掉$\frac{p_{\theta’}(\mathbf{s}_ t)}{p_{\theta}(\mathbf{s}_t)}$，理论上会导致有偏差，但实际效果还不错，因为两个策略足够接近时，这个比值不重要。以后会讲？？？？

4. 用自动求导做策略梯度法

目标函数的梯度为$\nabla_\theta J(\theta)\approx\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\left[\nabla_\theta\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{s}_ {i,t})\hat{Q}_ {i,t}\right]$。为了方便使用TensorFlow，可以构造损失函数$\tilde{J}(\theta)\approx\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{s}_ {i,t})\hat{Q}_ {i,t}$，$\hat{Q}_{i,t}$当成是权重，然后就可以自动求导。on-policy方法需要每更新一次梯度都进行重新采样，因此不能使用SGD。

实际使用时，由于方差较大，处理监督学习的一些技巧不一定适用。batch-size设置得越大越好。学习率的调整很有挑战性，ADAM通常是可行的。

总结

• $\nabla_\theta J(\theta) = \mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\left(\sum_{t=1}^T\nabla_\theta\log \pi_\theta(\mathbf{a}_ t\vert\mathbf{s}_ t)\right)\left(\sum_{t=1}^Tr(\mathbf{s}_t,\mathbf{a}_t)\right)\right]$
• 步骤：
  1. 运行策略$\pi_\theta(\mathbf{a}\vert \mathbf{s})$，蒙特卡洛采样抽取样本${\tau^i}$；
  2. 计算目标函数，估计梯度$\nabla_\theta J(\theta)\approx\frac{1}{N}\sum_{i=1}^N\left[\left(\sum_{t=1}^T\nabla_\theta\log \pi_\theta(\mathbf{a}_ {i,t}\vert \mathbf{s}_ {i,t})\right)\left(\sum_{t=1}^Tr(\mathbf{s}_ {i,t},\mathbf{a}_{i,t})\right)\right]$；
  3. 梯度上升$\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$。这里的$\nabla_\theta\log \pi_\theta(\mathbf{a}_t\vert \mathbf{s}_t)$与策略分布相关，如果策略网络的输出是一个高斯分布的均值-方差，那么该表达式在梯度更新时就是对高斯分布求导。
• 特点：
  • 不需要初始状态以及转移概率，即我们可以在任意环境中直接进行抽样生成样本
  • on-policy，导致数据利用率低
• 存在问题：
  • 有限采样导致高方差问题（收益值加上常数会引起策略变化）
  • 解决：
    1. 因果关系：当前策略不影响以前的reward函数，接近真实情况；
    2. baseline：收益值统一减去一个常数（如收益的平均）
• off-policy改进：
  • 直接重要性采样：会产生连乘，使梯度接近0
  • 对边际分布形式的目标函数进行两层重要性采样
• 实际中：梯度方差大，增大batch-size，用adam
• 网络：$s_i$输入网络$\pi$，根据输出分布得到（或随机选择）$a_i$，$r_i$，将$(s_i,a_i,r_i)$作为一组数据训练网络，网络会倾向于生成$r_i$较高的那种$a_i$。