马尔可夫决策过程
马尔可夫链$\mathcal{M}=\lbrace\mathcal{S},\mathcal{T}\rbrace$由状态空间$\mathcal{S}$和转移算子$\mathcal{T}$共同构成。令$\mu_{t,i}=p(s_t=i)$表示t时刻处于状态i概率,$\mathcal{T}_ {i,j}=p(s_{t+1}=i \vert s_t=j)$表示转移概率,则存在关系$\mu_{t+1}=\mathcal{T}\mu_t$。
马尔可夫决策过程$\mathcal{M}=\lbrace\mathcal{S},\mathcal{A},\mathcal{T},r\rbrace$,令$\mu_{t,j}=p(s_t=j)$,$\xi_{t,k}=p(a_t=k)$,转移算子$\mathcal{T}_ {i,j,k}=p(s_{t+1}=i \vert s_t=j,a_t=k)$,则存在关系$\mu_{t+1,i}=\sum_{j,k}\mathcal{T}_ {i,j,k}\mu_{t,j}\xi_{t,k}$。
增强学习的目标:$\pi_{\theta}(a \vert s)$由神经网络确定,输入状态$s$,得到行动$a$,环境通过转移概率$p(s’ \vert s,a)$得到新状态$s’$,形成循环。
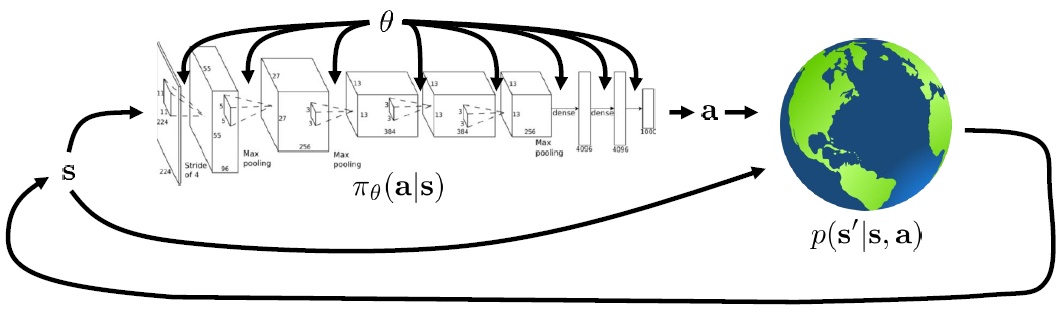
对于有限长轨迹$\tau=\lbrace \mathbf{s}_ 1,\mathbf{a}_ 1,\ldots,\mathbf{s}_ T,\mathbf{a}_ T \rbrace$,发生的概率为$p_\theta(\tau)=p(\mathbf{s}_ 1)\prod_{t=1}^T\pi_\theta(\mathbf{a}_ t \vert \mathbf{s}_ t)p(\mathbf{s}_ {t+1} \vert \mathbf{s}_ t,\mathbf{a}_ t)$。这个概率可以看做关于增广空间$(\mathbf{s},\mathbf{a})$的马尔可夫链,具体来说即为$p((\mathbf{s}_ {t+1},\mathbf{a}_ {t+1}) \vert (\mathbf{s}_ t,\mathbf{a}_ t))=p(\mathbf{s}_ {t+1} \vert \mathbf{s}_ t,\mathbf{a}_ t)\pi_\theta(\mathbf{a}_ {t+1} \vert \mathbf{s}_ {t+1})$。我们的优化目标是优化参数$\theta$,使得$\theta^*=\arg\max_\theta\mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\sum_tr(\mathbf{s}_t,\mathbf{a}_t)\right]$。
对于有限长轨迹问题,有$\left[\begin{array}{l}\mathbf{s}_ {t+1} \ \mathbf{a}_ {t+1}\end{array}\right]^T=\mathcal{T}\left[\begin{array}{l}\mathbf{s}_ t \ \mathbf{a}_ t\end{array}\right]^T$,进一步k步骤转移算子$\left[\begin{array}{l}\mathbf{s}_ {t+k} \ \mathbf{a}_ {t+k}\end{array}\right]^T=\mathcal{T}^k\left[\begin{array}{l}\mathbf{s}_ t \ \mathbf{a}_ t\end{array}\right]^T$。考虑$p_\theta(\mathbf{s}_ t,\mathbf{a}_ t)$是否逐渐收敛至平稳分布:所谓平稳分布指分布不发生变化,$\mu=\mathcal{T}\mu$,$\mu$是$\mathcal{T}$的特征值为1对应的特征向量。由于$\mathcal{T}$是一个随机矩阵,给定一些正则条件,这样的向量总是存在的,此时$\mu=p_\theta(\mathbf{s},\mathbf{a})$是其平稳分布。对于无限长度问题,对时间取极限时,它等于平稳分布下的情形。
补充:在RL中只关注期望,因为reward可能不连续,而reward在某种分布下的期望是连续的。
增强学习算法的一般步骤
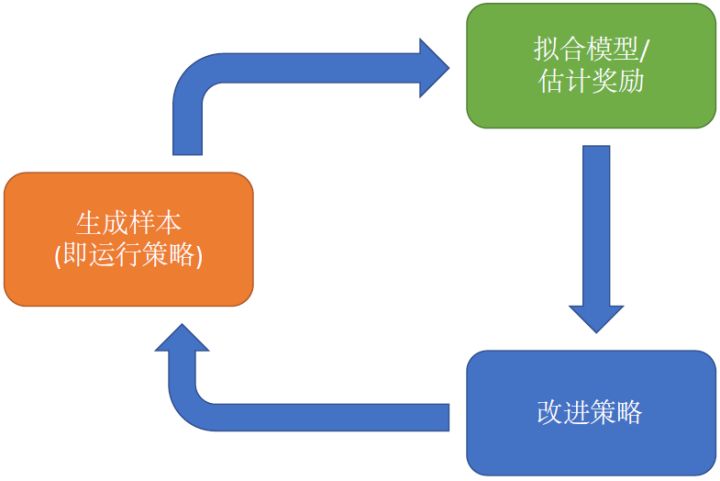
哪些步骤昂贵
取决于实际情况和具体算法:
- 生成数据:如果是真实物理系统,只能以一倍速度实时收集数据;如果使用MuJoCo之类的模拟器,可以实现加速;
- 第二步:策略梯度法求和容易,而Q-learning拟合网络复杂
- 第三步:Q-learning最大化行动容易,而基于模型反向传播优化相对困难
Q函数与值函数
Q函数:$Q^\pi(\mathbf{s}_ t,\mathbf{a}_ t)=\sum_{t’=t}^T\mathbf{E}_ {\pi_\theta}[r(\mathbf{s}_ {t’},\mathbf{a}_ {t’}) \vert \mathbf{s}_ t,\mathbf{a}_ t]$,给定$\mathbf{s}_t,\mathbf{a}_t$,未来总收益的条件期望。
值函数:$V^{\pi}(\mathbf{s}_ t)=\sum_{t’=t}^T\mathbf{E}_ {\pi_\theta}[r(\mathbf{s}_ {t’},\mathbf{a}_{t’})\vert \mathbf{s}_t]$,给定$\mathbf{s}_t$,未来总收益的条件期望。
关系:$V^\pi(\mathbf{s})=\mathbf{E}[Q^\pi(\mathbf{s},\mathbf{a})]$
我们想描述一个期望$\sum_{t=1}^T\mathbf{E}_ {(\mathbf{s}_ t,\mathbf{a}_ t)\sim p_\theta(\mathbf{ s}_ t,\mathbf{a}_ t)}r(\mathbf{s}_ t,\mathbf{a}_ t)$,将它替换成Q函数的形式$\mathbf{E}_ {\mathbf{s}_ 1\sim p(\mathbf{s}_ 1)}[\mathbf{E}_ {\mathbf{a}_ 1\sim \pi(\mathbf{a}_ 1 \vert \mathbf{s}_ 1)}[Q(\mathbf{s}_ 1,\mathbf{a}_ 1) \vert \mathbf{s}_ 1]]$。如果Q函数已知,策略改进将很简单,即$\pi(\mathbf{s}_ 1,\mathbf{a}_ 1)=I(\mathbf{a}_ 1=\arg\max_{\mathbf{a}_1}Q(\mathbf{s}_1,\mathbf{a}_1))$。
意义:
- 如果已知Q函数,总能找到一个策略使其最大化未来收益。
- 值函数代表了在策略$\pi(\mathbf{a}\vert \mathbf{s})$下的平均行动水平,如果$Q^{\pi}(\mathbf{s},\mathbf{a})>V^\pi(\mathbf{s})$就表明$\mathbf{a}$高于平均水平,就可以改进策略。
算法的权衡
目标函数:$\max_\theta\mathbf{E}_ {\tau\sim p_\theta(\tau)}\left[\sum_tr(\mathbf{s}_t,\mathbf{a}_t)\right]$
- 策略梯度法:表示目标函数,并对目标函数关于参数求梯度。本质是一阶最优化算法,求解无约束优化问题的通用方法。
- 值函数方法:用神经网络近似估计最优策略下的值函数或Q函数,并选择最大化函数的策略。注意此时策略并需要不显式表达出来,只需要选择使得Q函数最大的行动即可。
- actor-critic方法:用神经网络近似估计当前策略下的值函数或Q函数,并用这个信息求一个策略的梯度,改进当前的策略。所以也可以看作是策略梯度法和值函数方法的一个混合体。
- model-based方法:估计转移概率来作为模型,可以使用一系列方法改进策略:
- 抛弃策略,直接用模型去模拟:轨迹优化、最佳控制、蒙特卡洛树搜索
- 将梯度反向传播进策略(需要技巧)
- 使用模型学习Q函数和值函数:DP、无模型训练
????各种算法的整体总结,日后整理!!!!!!!!!!
采样效率:策略改变时是否需要重新采样样本。采样效率需要结合实际情况,比如有一个很快的模拟器,就可以使用进化算法,避免网络优化的时间。
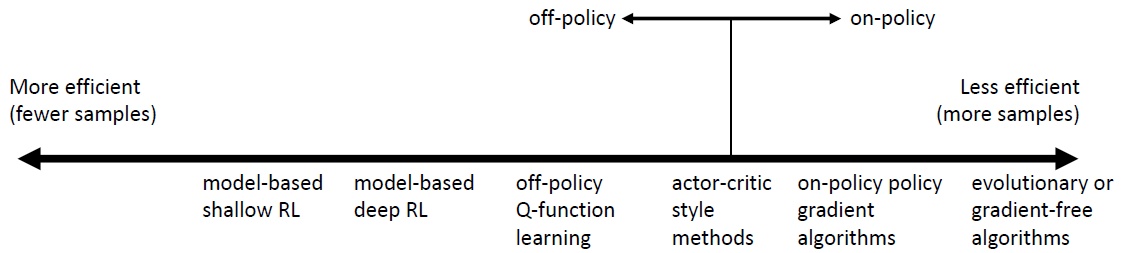
稳定性:通常不使用梯度下降法,因此算法不易收敛。
- Q-learning:不动点迭代,不易收敛
- model-based:模型并不优化期望函数
-
policy gradient:梯度下降,但样本效率低
- on-policy:改进的策略与生成数据的策略一致
- off-policy:改进的策略与生成数据的策略不一致