全概率公式:
这一节通过概率模型来对观察到的行为建模,引入软化操作,建立起概率推断和最优控制、强化学习之间的关系,可以用来在逆增强学习中使用观测推断收益函数。
概率图模型
回顾:最佳控制(optimal control)对人的行为建模
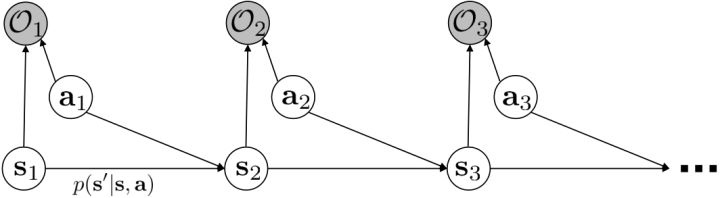
实际上人的决策并不完美,在某些领域有一些误差影响并不大,我们考虑使用概率图模型来表达某些“近似最优”的行为,即我们寻找最优控制,但某些次优的也可以考虑。使用$\mathcal{O}$表示最优变量的观测概率,对人“寻找最优的意图”进行建模。假设$\mathcal{O}$元素是一个0-1变量,如果在完成意图就是0,反之是1,也可以理解成一个事件。有一个重要假设$p(\mathcal{O}_ t\vert \mathbf{s}_ t,\mathbf{a}_ t)\propto\exp(r(\mathbf{s}_ t,\mathbf{a}_ t))$,对于$\tau=(\mathbf{s}_ {1:T},\mathbf{a}_{1:T})$,那么可以得到
它正比于轨迹发生的物理概率与总收益。$p(\tau)$仅表示轨迹发生的物理概率,与决策无关。在这里,收益最大的轨迹就变得可能性最大;如果有多条轨迹收益一样大,那么它们有相同的可能性。这种模型有几个好处:1. 对次优行为进行建模,在逆增强学习中非常有意义,用于观察他人的行为来揣测他的真实目标;2. 可以使用一些推断算法来求解控制规划问题;3. 可以对为什么会偏好随机行为(相较于确定性行为)给出解释
推断(inference)
后向信息
后向信息$\bbox[5px,border:2px solid red]{\beta_t(\mathbf{s}_ t,\mathbf{a}_ t)=p(\mathcal{O}_{t:T}|\mathbf{s}_t,\mathbf{a}_t)}$,表示给定某个时间点的状态和行动,得出未来最优性变量的观测概率(它不关心过去)。之所以说是后向信息,是它的计算方式类似于LQR中的倒推。在递推边界$t=T$时,根据定义有$\beta_T(\mathbf{s}_T,\mathbf{a}_T)=p(\mathcal{O}_T|\mathbf{s}_T,\mathbf{a}_T)\propto\exp(r(\mathbf{s}_T,\mathbf{a}_T))$;在中间有
其中第二项$p(\mathbf{s}_ {t+1}\vert\mathbf{s}_ t,\mathbf{a}_ t)$已知;第三项$p(\mathcal{O}_ t\vert\mathbf{s}_ t,\mathbf{a}_ t)\propto\exp(r(\mathbf{s}_ t,\mathbf{a}_ t))$;第一项全概率展开有
其中$p(\mathbf{a}_ {t+1}\vert\mathbf{s}_ {t+1})$比较奇怪,它并不是一个策略函数,而只是一个给定状态做出什么决策的先验概率,在这里我们可以先认为是均匀分布的。具体倒推算法如下:
for $t=T-1$ to 1:
$\qquad\beta_t(\mathbf{s}_ t,\mathbf{a}_ t)=p(\mathcal{O}_ t\vert \mathbf{s}_ t,\mathbf{a}_ t)\mathbf{E}_ {\mathbf{s}_ {t+1}\sim p(\mathbf{s}_ {t+1}\vert\mathbf{s}_ t,\mathbf{a}_ t)}[\beta_{t+1}(\mathbf{s}_ {t+1})] $
$\qquad\beta_t(\mathbf{s}_ t)=\mathbf{E}_ {\mathbf{a}_ t\sim p(\mathbf{a}_ t\vert\mathbf{s}_ t)}[\beta_ t(\mathbf{s}_ t,\mathbf{a}_ t)]$
注释1
这个算法与值函数迭代(value iteration)算法不谋而合。令$\bbox[5px,border:2px solid red]{V_t(\mathbf{s}_ t)=\log \beta_t(\mathbf{s}_ t)}$,$\bbox[5px,border:2px solid red]{Q_t(\mathbf{s}_ t,\mathbf{a}_ t)=\log \beta_t(\mathbf{s}_ t,\mathbf{a}_ t)}$。根据第二条有$V_t(\mathbf{s}_ t)=\log\int\exp(Q_t(\mathbf{s}_ t,\mathbf{a}_ t))\mathrm{d}\mathbf{a}_ t$,随着Q的值变大,会有$V_t(\mathbf{s}_ t)\rightarrow\max_{\mathbf{a}_ t}Q_t(\mathbf{s}_ t,\mathbf{a}_ t)$。(后者为标准max操作,而前者被称为softmax;后续会介绍相关软化操作其实就是引入次优策略,避免陷入局部最优)根据第一条关系,有$Q_ t(\mathbf{s}_ t,\mathbf{a}_ t)=r(\mathbf{s}_ t,\mathbf{a}_ t)+\log\mathbf{E}[\exp(V_ {t+1}(\mathbf{s}_ {t+1}))]$,这是随机状态转移情况;如果是确定状态转移,有$Q_t(\mathbf{s}_ t,\mathbf{a}_ t)=r(\mathbf{s}_ t,\mathbf{a}_ t)+V_{t+1}(\mathbf{s}_{t+1})$。
注释2
对于$p(\mathbf{a}_ {t+1}\vert\mathbf{s}_ {t+1})$,我们假设它是均匀分布。对于不均匀分布,$V_t(\mathbf{s}_ t)=\log\int\exp(Q_t(\mathbf{s}_ t,\mathbf{a}_ t)+\log p(\mathbf{a}_ t\vert\mathbf{s}_ t))\mathrm{d}\mathbf{a}_ t$,令新的Q函数为$\tilde{Q}_ t(\mathbf{s}_ t,\mathbf{a}_ t)=r(\mathbf{s}_ t,\mathbf{a}_ t)+\log p(\mathbf{a}_ t\vert\mathbf{s}_ t)+\mathbf{E}[V_{t+1}(\mathbf{s}_ {t+1})]$,则$V_t(\mathbf{s}_ t)=\log\int\exp(\tilde Q_t(\mathbf{s}_ t,\mathbf{a}_ t))\mathrm{d}\mathbf{a}_ t$关系不变。因此,实际求解的时候可以不失一般性地假设$p(\mathbf{a}_ {t+1}\vert\mathbf{s}_{t+1})$不对算法产生任何困难:如果有一个非均匀分布的先验,就把它放到收益函数里面去就行了。
策略
策略$\bbox[5px,border:2px solid red]{\pi(\mathbf{a}_ t|\mathbf{s}_ t)=p(\mathbf{a}_ t|\mathbf{s}_ t,\mathcal{O}_ {1:T})}$,表示给定当前状态和所有最优性变量,得出行动的概率,具有马尔可夫性,即$\pi(\mathbf{a}_ t|\mathbf{s}_ t)=p(\mathbf{a}_ t|\mathbf{s}_ t,\mathcal{O}_{t:T})$。对式子变形有:
假设先验$p(\mathbf{a}_t\vert\mathbf{s}_t)$为均匀分布,则有
即$\bbox[5px,border:2px solid red]{A_t(\mathbf{s}_t,\mathbf{a}_t) = log(\pi(\mathbf{a}_t\vert\mathbf{s}_t))}$,正好引出优势函数的概念。这样的策略的一个直接的解释是,使得“更好的”行动更可能发生。如果有多个性质一样好的行动,它们的可能性一致,只是一个概率分布的策略只需随机挑选一个。
前向信息
前向信息$\bbox[5px,border:2px solid red]{\alpha_t(\mathbf{s}_ t)=p(\mathbf{s}_ t|\mathcal{O}_{1:t-1})}$,表示给定之前的所有最优性变量,得出在当前时点到达某状态的概率。这个对策略来说并不重要,但是在逆增强学习中非常重要。
其中,第一项是已知的系统状态转移,$p(\mathbf{a}_ {t-1}\vert\mathbf{s}_ {t-1},\mathcal{O}_ {t-1})\propto\exp(r(\mathbf{s}_ {t-1},\mathbf{a}_ {t-1}))$,$p(\mathbf{a}_ {t-1}\vert\mathbf{s}_{t-1})$是均匀分布,分母也是一个归一化常数。
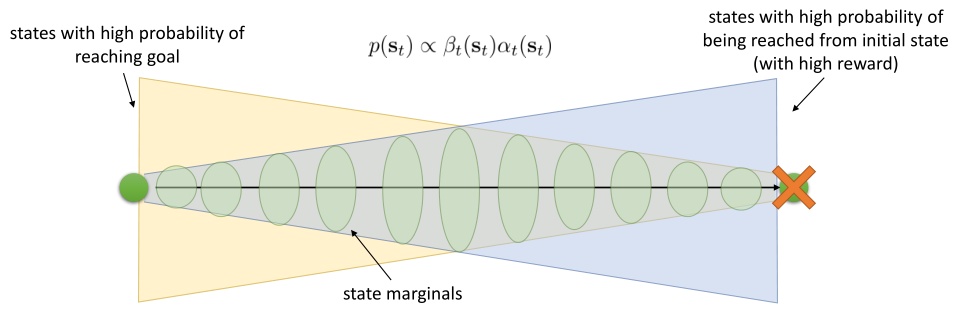
有了前向消息和后向信息之后,给定所有最优性变量,求某时刻的某状态的发生概率就比较容易了。可以得到:
这个概率是前向消息和后项消息的乘积,可以说是一个交汇。考虑上图左边圆点是起点,右边叉叉是终点的路径。黄色锥区域是能够有高概率到达终点的状态,蓝色锥区域是有高概率从初始状态以高收益到达的状态,然后基本上就是两者的交(概率上相乘)。
软化的增强学习算法(softmax)
软化Q学习
软化Q学习和标准Q学习相比,目标值函数变成了$V(\mathbf{s}’)=\text{soft}\max_{\mathbf{a}’}Q_\phi(\mathbf{s}’,\mathbf{a}’)=\log\int\exp(Q_\phi(\mathbf{s}’,\mathbf{a}’))\mathrm{d}\mathbf{a}’$,策略函数也变成了类似Boltzmann探索的$\pi(\mathbf{a}|\mathbf{s})=\exp(Q_\phi(\mathbf{s},\mathbf{a})-V(\mathbf{s}))=\exp(A(\mathbf{s},\mathbf{a}))$。因此,和标准的DQN相比,只需要将第三步由$y_j=r_j+\gamma\max_{\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_ j’,\mathbf{a}_ j’)$改成$y_j=r_j+\gamma\text{ soft}\max_ {\mathbf{a}_ j’}Q_{\phi’}(\mathbf{s}_j’,\mathbf{a}_j’)$即可。
软化策略梯度法
结论是:如果要对策略梯度法进行软化,只需要在目标函数内,在期望收益之后加上策略函数的熵就可以了:这个熵给策略一定压力,使得它不会退化成一个确定性策略。这种方法通常被称为熵正则化(entropy regularized)策略梯度法,通常用于防止策略过早地熵崩塌(premature entropy collapse)。(可以理解为强化学习一旦发现一块比较好的区域就会加强这块区域的利用率,容易陷入局部最优。)在策略梯度法的第二个问题中提到,高斯策略下,策略梯度法通常希望减少策略的方差,因为减少方差通常可以导致局部的收益增大,但这同时也会使得策略梯度卡住,改进停止,加入熵也是一个方法。
软化方法的优点:
- 增加探索,防止熵的坍塌
- 覆盖更多的状态,鲁棒性更强
- 对于并列最优的情况会得到一个分部,更适合对人的行为建模