Table of Contents
基本图算法
DFS
例子:走迷宫
bool visited[50][50];
int grid[50][50];
int N;
int dirs[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };
bool dfs(int height, int i, int j){
if (grid[i][j] > height) // 额外限制条件
return false;
if (visited[i][j])
return false;
if (i==N-1 && j==N-1) // 终点条件
return true;
visited[i][j] = true;
for(int k=0; k<4; k++){
int ii = i+dirs[k][0];
int jj = j+dirs[k][1];
if(ii >= 0 && ii < N && jj >= 0 && jj < N){
bool ret = dfs(height, ii, jj);
if(ret)
return ret;
}
}
// visited[i][j] = false; // 注意!!!
return false;
}
int main() {
memset(visited, false, 50 * 50 * sizeof(bool));
dfs(10, 0, 0);
}
注意:
- 在回溯法函数中,先处理各种限制条件和终点条件,再直接调用子函数,最后处理子函数的返回结果。
- 图中某些节点会访问多次。如果每次访问结果都一致,用
visited做标志位缓存中间结果,在函数开头置为true;如果每次访问结果不一致,不能用visited做标志位缓存中间结果。 - 在树中,每个节点仅访问一次,没必要使用
visited。
有向无环图的拓扑排序
算法导论的方法
深度优先搜索时加入每个点的访问结束时间,按结束时间逆排序。
class Solution(object):
visited = None
f_time = None
time = None
def DFS(self, n, edges):
graph = [[] for _ in range(n)]
for item in edges:
graph[item[0]].append(item[1])
self.visited = [0] * n
self.time = 0
self.f_time = [0] * n
for i in range(n):
if not self.visited[i]:
try:
self.DFS_visit(graph, i)
except:
return []
ret = zip(self.f_time, range(n))
ret = sorted(ret, key=lambda x: x[0])[::-1]
return [item[1] for item in ret]
def DFS_visit(self, graph, i):
self.time += 1
self.visited[i] = 1
for j in graph[i]:
if not self.visited[j]:
self.DFS_visit(graph, j)
elif self.visited[j] == 1:
raise
self.visited[i] = -1
self.time += 1
self.f_time[i] = self.time
另一种数据结构
构建邻接链表,以起点或终点为基准均可以。构建队列,将入度为0的加入队列,进行广度优先搜索。
int main(){
int n, m, k;
cin >> n >> m >> k;
vector<int> indegree(n + 1, 0);
vector<int> value(n + 1, 0); // 初始值
vector<vector<int>> graph(n + 1,vector<int>()); // 邻接链表
for (int i = 1;i <= m;++i){
int u, v;
cin >> u >> v;
graph[u].push_back(v);
indegree[v]++;
}
queue<int> q;
for (int i = 1;i <= n;++i){ // 入度为0,加入队列
if (indegree[i] == 0)
q.push(i);
}
while (!q.empty()){
int v = q.front();
q.pop();
for (auto u : graph[v]){
// 更新值
if (--indegree[u] == 0) // 入度为0,加入队列
q.push(u);
}
}
// 遍历结果
}
应用:可以统计图中每个点的访问次数,复杂度$O(m+n)$
图与树
无向图是树
Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether these edges make up a valid tree.
思路:一棵树必须具备如下特性:
- 是一个全连通图(所有节点相通)
- 无回路
public class Solution {
public boolean validTree(int n, int[][] edges) {
if (edges.length != n-1) return false;
int[] roots = new int[n];
for(int i=0; i<n; i++) roots[i] = i;
for(int i=0; i<edges.length; i++) {
int root1 = root(roots, edges[i][0]);
int root2 = root(roots, edges[i][1]);
if (root1 == root2) return false;
roots[root2] = root1;
}
return true;
}
private int root(int[] roots, int id) {
if (id == roots[id]) return id;
return root(roots, roots[id]);
}
}
Union-Find
int N;
const int MAX_SIZE = 100010;
int root[MAX_SIZE];
int get(int id){
if(id == root[id])
return id;
return get(root[id]);
}
int main() {
cin >> N;
int cnt = 0;
for(int i=0; i<MAX_SIZE; i++)
root[i] = i;
vector<string> ret;
while(N--){ // n组数据
int choose;
int id1, id2;
cin >> choose >> id1 >> id2;
if(choose == 0){ // 在线设置
int root1 = get(id1);
int root2 = get(id2);
root[root2] = root1;
}else{ // 在线查询
int root1 = get(id1);
int root2 = get(id2);
if (root1 == root2)
ret.push_back("yes");
else
ret.push_back("no");
}
}
for_each(ret.begin(), ret.end(), [](string s){ cout << s << endl; });
};
有向图是树
深度优先遍历,记录每个节点访问次数visited:
0:未访问
1:访问一次
2:访问多次
当下一个要访问的点为1时,表示存在后向边,即存在环,直接抛出异常,返回False
class Solution(object):
visited = None
def DFS(self, n, edges):
graph = [[] for _ in range(n)]
for item in edges:
graph[item[0]].append(item[1])
self.visited = [0] * numCourses
for i in range(n):
if not self.visited[i]:
try:
self.DFS_visit(graph, i)
except:
return False
return True
def DFS_visit(self, graph, i):
self.visited[i] = 1
for j in graph[i]:
if not self.visited[j]:
self.DFS_visit(graph, j)
elif self.visited[j] == 1:
raise
self.visited[i] = -1
最小生成树
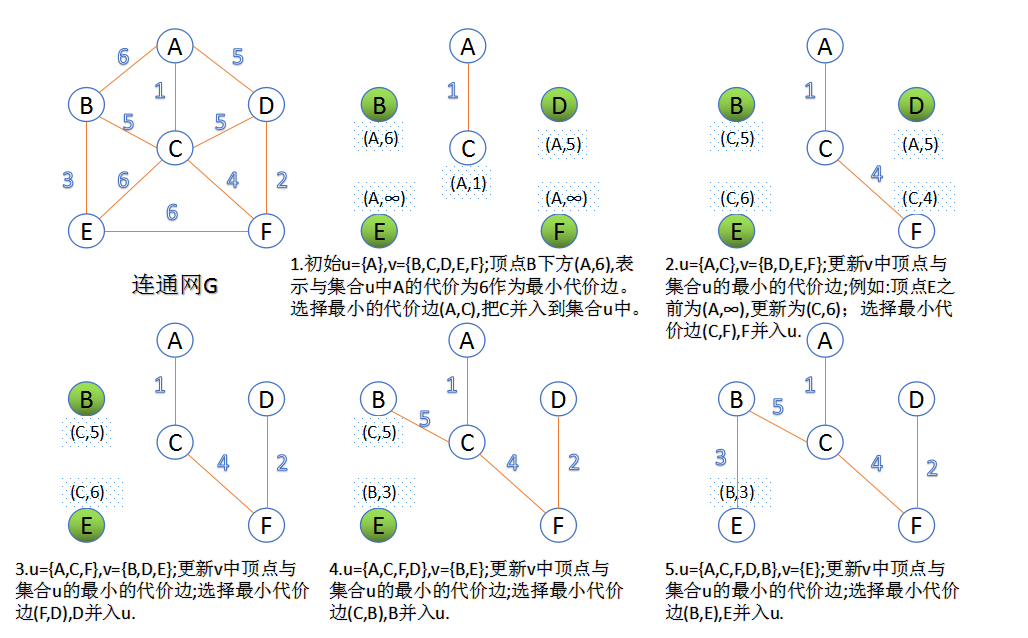
Prim
思路:从已选点的临接边中选择权值最小的边作为树边。
复杂度:O(V^2),使用堆能达到O(VlgV)
int N, cost[1001], graph[1001][1001];
bool use[1001];
int prim(){
// graph: 邻接矩阵
// cost: 每个点的最小权重
// 输出: 路径总长度
int ans = 0;
for(int i = 0; i < N; ++i){
cost[i] = graph[0][i];
}
use[0] = true;
for(int i = 1; i < N; ++i){
int minn = INF, minj;
for(int j = 1; j < N; ++j){ // 根据cost寻找最短路径
if(!use[j] && cost[j] > 0 && cost[j] < minn){
minn = cost[j];
minj = j;
}
}
use[minj] = true;
ans += minn; // 增加路径
for(int j = 1; j < N; ++j){ // 得到最短路径后更新cost
if(!use[j] && graph[minj][j] > 0 && graph[minj][j] < cost[j]){
cost[j] = graph[minj][j];
}
}
}
return ans;
}
int main(){
cin >> N;
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
cin >> graph[i][j];
prim();
};
kruskal
思路:从全局找权值最小的边
特点:适合稀疏图,实现比prim简单

const int MAX = 1000010;
struct EDGE {
int u, v, w;
bool operator < (const EDGE& p)const
{
return w < p.w;
}
}Edge[MAX];
int root[MAX];
int get(int id) {
if(id == root[id])
return root[id];
return get(root[id]);
}
void Union(int u, int v) {
if(u>v) swap(u, v);
root[v] = root[u];
}
void Kruscal(int M) {
// M: edge
// root: union-find
ll ans = 0;
for(int i = 1; i <= M; i++) {
int u, v;
if((u = get(Edge[i].u)) != (v = get(Edge[i].v))) {
Union(u, v);
ans += Edge[i].w;
}
}
cout << ans;
}
int main() {
int N, M;
cin >> N >> M;
for(int i = 1; i <= N; i++)
root[i] = i;
for(int i = 1; i <= M; i++)
cin >> Edge[i].u >> Edge[i].v >> Edge[i].w;
sort(Edge+1, Edge+M+1);
Kruscal(M);
return 0;
}
最短路径
单源最短路径 Dijkstra
Dijkstra算法:非负权重有向图上单源最短路径
复杂度:O(V^2)

vector<int> dist;
unordered_map<int, vector<pair<int, int>>> graph;
bool seen[101]={false};
int Dijkstra(int N, int S, int E) {
// N: vertex
// S: start node
// E: end node
// graph: node -> [(node, weight)...]
// seen
// dist
for(int i = 0; i <= N; i++)
dist.push_back(numeric_limits<int>::max());
dist[S] = 0;
while(true){
int candNode = -1;
int candDist = numeric_limits<int>::max();
for(int i = 1; i <= N; i++){
if(!seen[i] && dist[i] < candDist){
candDist = dist[i];
candNode = i;
}
}
if(candNode<0)
break;
seen[candNode] = true;
if(graph.find(candNode)!=graph.end()){
for(pair<int, int> p: graph.find(candNode)->second){
dist[p.first] = min(dist[p.first], dist[candNode]+p.second);
}
}
}
return dist[E];
}
所有节点对的最短路径 Floyd
设$d_{ij}^{(k)}$为从节点i到节点j所有中间节点取自${1,2,…,k}$的一条最短路径。根据动态规划得到递推式:
复杂度:O(V^3)
int edge[101][101];
int main() {
memset(edge, 0x3f, 101 * 101 * sizeof(int));
int N, M;
cin >> N >> M;
for(int i=0; i<M; i++){
int a,b,c;
cin >> a >> b >> c;
if (edge[a][b] > c)
edge[a][b] = edge[b][a] = c;
}
for (int k = 1; k <= N; ++k) {
for (int j = 2; j <= N; ++j) {
edge[j][j] = 0;
for (int i = 1; i < j; ++i) {
if (k != i && k != j) {
int value = edge[i][k] + edge[k][j];
edge[j][i] = edge[i][j] = (edge[i][j] > value ? value : edge[i][j]);
}
}
}
}
// output: edge
return 0;
}
单源最短路径 SPFA
SPFA: Shortest Path Faster Algorithm
const int N = 1e5 + 10;
const int M = 1e6 + 10;
int CNT;
int before[N]; // 上一条以i为起点的边
int dis[N];
struct Edge {
int t; // 终点
int n; // 上一条同样起点的边
int weight;
} edge[M << 1];
void insert(int from, int to, int weight) {
edge[CNT].t = to;
edge[CNT].weight = weight;
edge[CNT].n = before[from];
before[from] = CNT++;
edge[CNT].t = from;
edge[CNT].weight = weight;
edge[CNT].n = before[to];
before[to] = CNT++;
}
bool relax(int &a, int b) { return a > b ? (a = b, true) : false; }
int disj(int s, int e) {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pqueue;
dis[s] = 0;
pqueue.push(pair<int, int>(0, s));
while (!pqueue.empty()) {
int prev = pqueue.top().second;
int d = pqueue.top().first;
pqueue.pop();
if (dis[prev] < d)
continue;
if (prev == e)
return d;
for (int i = before[prev], x; ~i; i = edge[i].n) {
x = edge[i].t;
if (relax(dis[x], edge[i].weight + d))
pqueue.push(pair<int, int>(dis[x], x));
}
}
return dis[e];
}
int main() {
int n, m, s, e;
cin >> n >> m >> s >> e;
fill(before, before + n + 1, -1);
fill(dis, dis + n + 1, INF);
int u, v, w;
for (int i = 0; i < m; i++) {
cin >> u >> v >> w;
insert(u, v, w);
}
cout << disj(s, e) << endl;
return 0;
}
二分图
二分图的判定
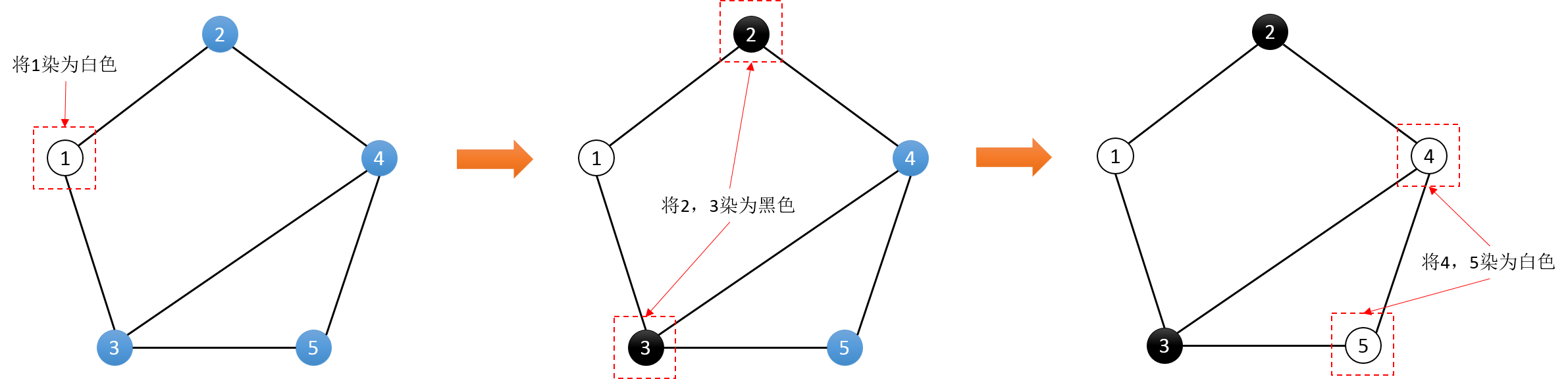
思路:
- 选取一个未染色的点u进行染色
- 遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并重复;若v已经染色,如果u和v颜色相同,判定不可行。
- 若所有节点均已染色,则判定可行。
const int MAXN = 10000 + 10;
int N, M; // N点、M边
int color[MAXN]; // 颜色
vector<int> G[MAXN]; // 图
bool dfs(int x){ // dfs
for(int i = 0; i < G[x].size(); ++i){
int t = G[x][i];
if(color[x] == color[t]) // 颜色相同,返回false
return false;
if(!color[t]){
color[t] = 3 - color[x]; // 染不同颜色
if(!dfs(t))
return false;
}
}
return true;
}
bool solve(){
for(int i = 1; i <= N; ++i){
if(!color[i]){
color[i] = 1;
if(!dfs(i)) return false;
}
}
return true;
}
int main(){
int T;
cin >> T;
while(T--){
cin >> N >> M;
memset(color, 0, sizeof(color));
for(int i = 1; i <= N; ++i)
G[i].clear();
int u, v;
while(M--){
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
if(solve()){
cout << "Correct" << endl;
}else{
cout << "Wrong" << endl;
}
}
return 0;
}
二分图最大匹配
概念
- 匹配(matching)是一个边集,满足边集中的边两两不邻接。最大匹配是一个图所有匹配中,所含匹配边数最多的匹配。
- 交错轨(alternating path)是图的一条简单路径,满足任意相邻的两条边,一条在匹配内,一条不在匹配内。增广轨(augmenting path)是一个始点与终点都为未匹配点的交错轨。增广路的一个重要特点是非匹配边比匹配边多一条,可以用来改进匹配。
- 增广轨定理:一个匹配是最大匹配当且仅当没有增广轨。
匈牙利算法
根据一个匹配是最大匹配当且仅当没有增广路,求最大匹配就是找增广轨,直到找不到增广轨,就找到了最大匹配。
从G中找出一个未匹配点v,如果没有则算法结束,否则,以v为起点,查找增广路(邻接点是为未匹配点,则返回寻找完成,若v的邻接点u是匹配点,则从u开始查找,直至查找到有未匹配点终止),如果没有找到增广路,则算法终止。
举例:1->2->0->4->3
dfs(0),找到匹配0->2,返回,不会遍历0->4dfs(1),找到匹配1->2,2已经被匹配,因此对2的匹配点重新dfs(0)。若有匹配点1->2->0->4,cnt加1。(类似于交错路径0->2取反形成1->2->0->4)
vector<int> G[1000]; // 图
int f[1000]; // 点对应的匹配点
bool vis[1000]; // 点访问过
bool dfs(int i) {
vis[i] = 1;
for (int j = 0; j < (int) G[i].size(); ++j)
// 情况1:邻接点v没有匹配
// 情况2:邻接点v是u的匹配点,从v开始查找
if (f[G[i][j]] == -1 || (!vis[f[G[i][j]]] && dfs(f[G[i][j]]))) {
f[G[i][j]] = i;
f[i] = G[i][j];
return 1;
}
return 0;
}
int main() {
int N, M;
cin >> N >> M;
memset(f, -1, sizeof(f));
while (M--) {
int u, v;
scanf("%d%d", &u, &v);
--u, --v;
G[u].push_back(v);
G[v].push_back(u);
}
int cnt = 0;
for (int i = 0; i < N; ++i) {
if (f[i] == -1) { // i没有匹配,开始查找
memset(vis, 0, sizeof(vis));
cnt += dfs(i);
}
}
printf("%d\n", cnt);
}
欧拉图
- 无向图欧拉回路:所有顶点的度数都为偶数。
- 有向图欧拉回路:所有顶点的出度与入读相等。
- 无向图欧拉路径: 至多有两个顶点的度数为奇数,其他顶点的度数为偶数。
- 有向图欧拉路径: 至多有两个顶点的入度和出度绝对值差1(若有两个这样的顶点,则必须其中一个出度大于入度,另一个入度大于出度),其他顶点的入度与出度相等。
哈密顿回路:经过所有点一次。NP完全问题,有时可以通过点-->线转换成欧拉回路。
graham scan
寻找凸包,时间复杂度$O(nlogn)$
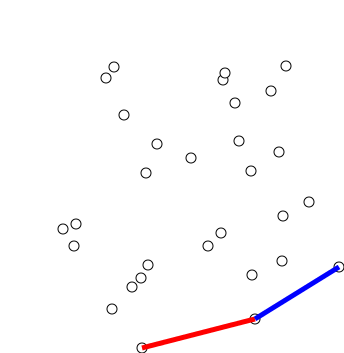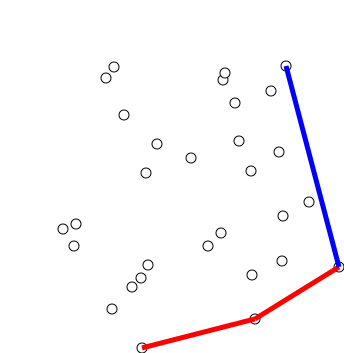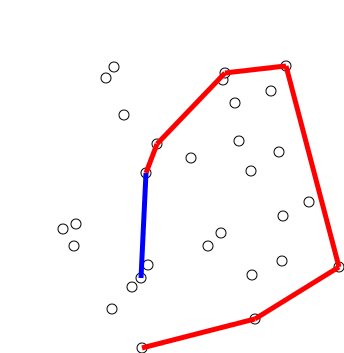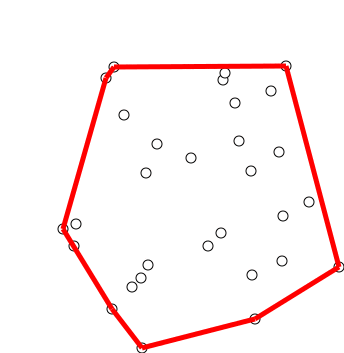
步骤:
- 按Y坐标对点排序,Y坐标最低点为Y0(Y相同则取X最小点)
- 剩下点按与Y0的极角的逆时针顺序排序,角度相同则忽略与Y0较近的点(欧氏距离)
- 将Y0,Y1,Y2压入栈stack
- 循环取Yi,栈顶元素top1,top2,若top2,top1,Yi没有向左转,则弹出top,直到满足条件,压入Yi
- 输出stack
struct node {
int x;
int y;
int id;
} node[100005], output[100005];
int n;
int cross(node p0, node p1, node p2) {
//计算叉乘,注意p0,p1,p2的位置,这个决定了方向
return (int)(p1.x-p0.x)*(p2.y-p0.y)-(int)(p1.y-p0.y)*(p2.x-p0.x);
}
int dis(node a, node b) {
//计算距离,这个用在了当两个点在一条直线上
return(int)(a.x-b.x)*(a.x-b.x)+(int)(a.y-b.y)*(a.y-b.y);
}
bool cmp(node p1, node p2) {
//极角排序
int z = cross(node[0], p1, p2);
if( z>0 || (z==0 && dis(node[0],p1) < dis(node[0],p2)))
return 1;
return 0;
}
void Graham() {
int k=0;
for(int i=0; i<n; i++)
if(node[i].y<node[k].y || (node[i].y==node[k].y&&node[i].x<node[k].x))
k = i;
swap(node[0], node[k]); //找左下的点p0
sort(node+1, node+n, cmp); //以node[0]为基点排序
int top = 1;
output[0] = node[0];
output[1] = node[1];
for(int i=2; i<n; i++) { //控制进栈出栈
while(cross(output[top-1], output[top], node[i]) < 0 && top)
top--;
top++;
output[top] = node[i];
}
}
int main() {
cin >> n;
for(int i=0; i<n; i++) {
cin >> node[i].x >> node[i].y;
node[i].id = i;
}
Graham();
}