最长回文子串——Manacher 算法

March 5th, 2017

1. 解决长度奇偶性带来的对称轴位置问题

Manacher算法首先对字符串做一个预处理，在所有的空隙位置(包括首尾)插入同样的符号，要求这个符号是不会在原串中出现的。这样会使得所有的串都是奇数长度的。以插入#号为例：

aba  ———>  #a#b#a#
abba ———>  #a#b#b#a#

2. 解决重复访问的问题

我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。Manacher定义了一个回文半径数组RL，用RL[i]表示以第i个字符为对称轴的回文串的回文半径。我们一般对字符串从左往右处理，因此这里定义RL[i]为第i个字符为对称轴的回文串的最右一个字符与字符i的距离。对于上面插入分隔符之后的两个串，可以得到RL数组：

char:    # a # b # a #
 RL :    1 2 1 4 1 2 1
RL-1:    0 1 0 3 0 1 0
  i :    0 1 2 3 4 5 6

char:    # a # b # b # a #
 RL :    1 2 1 2 5 2 1 2 1
RL-1:    0 1 0 1 4 1 0 1 0
  i :    0 1 2 3 4 5 6 7 8

通过观察可以发现，RL[i]-1的值，正是在原本那个没有插入过分隔符的串中，以位置i为对称轴的最长回文串的长度。那么只要我们求出了RL数组，就能得到最长回文子串的长度。怎样高效地求的RL数组？基本思路是利用回文串的对称性，扩展回文串。

1）当i在MaxRight的左边

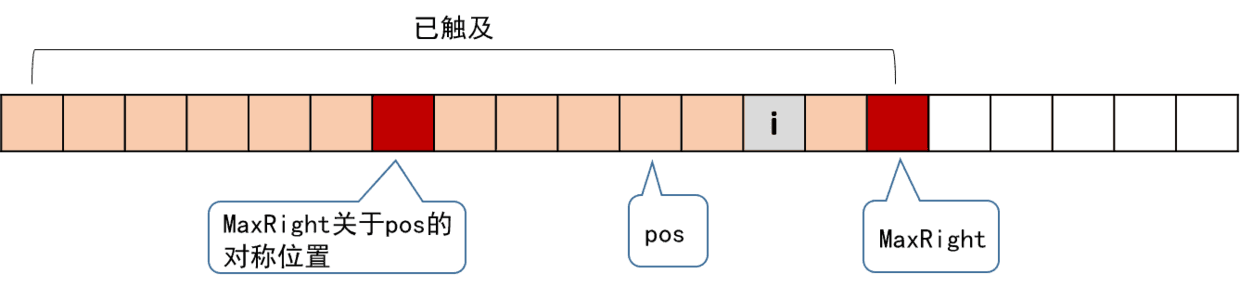
我们知道，图中两个红色块之间（包括红色块）的串是回文的；并且以i为对称轴的回文串，是与红色块间的回文串有所重叠的。我们找到i关于pos的对称位置j，这个j对应的RL[j]我们是已经算过的。根据回文串的对称性，以i为对称轴的回文串和以j为对称轴的回文串，有一部分是相同的。

我们知道RL[i]至少不会小于RL[j]，并且已经知道了部分的以i为中心的回文串，于是可以令RL[i]=RL[j]。但是以i为对称轴的回文串可能实际上更长，因此我们试着以i为对称轴，继续往左右两边扩展，直到左右两边字符不同，或者到达边界。

1）当i在MaxRight的右边

遇到这种情况，说明以i为对称轴的回文串还没有任何一个部分被访问过，于是只能从i的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。然后更新MaxRight和pos。

3. 算法实现

def manacher(s):
    s='#'+'#'.join(s)+'#'

    RL=[0]*len(s)
    MaxRight=0
    pos=0
    MaxLen=0
    for i in range(len(s)):
        if i<MaxRight:
            RL[i]=min(RL[2*pos-i], MaxRight-i)
        else:
            RL[i]=1
        #尝试扩展，注意处理边界
        while i-RL[i]>=0 and i+RL[i]<len(s) and s[i-RL[i]]==s[i+RL[i]]:
            RL[i]+=1
        #更新MaxRight,pos
        if RL[i]+i-1>MaxRight:
            MaxRight=RL[i]+i-1
            pos=i
        #更新最长回文串的长度
        MaxLen=max(MaxLen, RL[i])
    return MaxLen-1

public int manacher(String s) {
    String s1 = "#" + String.join("#", s.split("")) + "#";
    int[] RL = new int[s1.length()];
    int MaxRight = 0, pos = 0, MaxLen = 0;

    for(int i = 0; i < s1.length(); i++){
        if(i < MaxRight)
            RL[i]=Math.min(RL[2*pos-i], MaxRight-i);
        else
            RL[i]=1;

        while(i-RL[i]>=0 && i+RL[i]<s1.length() && s1.charAt(i-RL[i])==s1.charAt(i+RL[i]))
            RL[i]+=1;

        if(RL[i]+i-1>MaxRight) {
            MaxRight = RL[i] + i - 1;
            pos = i;
        }
        MaxLen=Math.max(MaxLen, RL[i]);
    }
    return MaxLen - 1;
}

4. 复杂度分析

空间复杂度：插入分隔符形成新串，占用了线性的空间大小；RL数组也占用线性大小的空间，因此空间复杂度是线性的。

时间复杂度：尽管代码里面有两层循环，通过amortized analysis我们可以得出，Manacher的时间复杂度是线性的。由于内层的循环只对尚未匹配的部分进行，因此对于每一个字符而言，只会进行一次，因此时间复杂度是O(n)。

ShengYg

Step after step the ladder is ascended.

Tags • string